题目内容
12.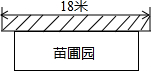 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
分析 (1)根据题意得方程求解即可;
(2)设苗圃园的面积为y,根据题意得到二次函数解析式y=x(30-2x)=-2x2+30x,根据二次函数的性质求解即可;
(3)由题意得不等式,即可得到结论.
解答 解:(1)根据题意得:(30-2x)x=72,
解得:x=3,x=12,
∵30-2x≤18,
∴x=12;
(2)设苗圃园的面积为y,
∴y=x(30-2x)=-2x2+30x,
∵a=-2<0,
∴苗圃园的面积y有最大值,
∴当x=$\frac{15}{2}$时,即平行于墙的一边长15>8米,y最大=112.5平方米;
∵6≤x≤11,
∴当x=11时,y最小=88平方米;
(3)由题意得:-2x2+30x≥100,
∵30-2x≤18
解得:6≤x≤10.
点评 此题考查了二次函数、一元二次方程、一元二次不等式的实际应用问题.解题的关键是根据题意构建二次函数模型,然后根据二次函数的性质求解即可.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
20.计算x4÷x+x3的结果是( )
| A. | x4 | B. | x3 | C. | 2x3 | D. | 2x4 |
1.下列运算正确的是( )
| A. | a2+a3=a5 | B. | (a+2b)2=a2+2ab+b2 | C. | a6÷a3=a2 | D. | (-2a3)2=4a6 |
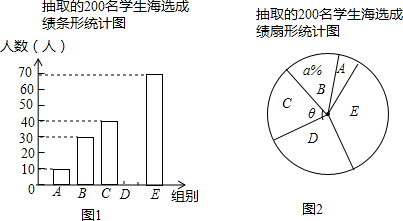
2.中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为15,表示C组扇形的圆心角θ的度数为72度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
抽取的200名学生海选成绩分组表
| 组别 | 海选成绩x |
| A组 | 50≤x<60 |
| B组 | 60≤x<70 |
| C组 | 70≤x<80 |
| D组 | 80≤x<90 |
| E组 | 90≤x<100 |
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为15,表示C组扇形的圆心角θ的度数为72度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?

 如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.