题目内容
13.在一次数学游戏中,老师在A、B、C三个盘子里分别放了一些糖果,糖果数依次为a0,b0,c0,记为G0=(a0,b0,c0).游戏规则如下:若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作.若三个盘子中的糖果数都相同,游戏结束.n次操作后的糖果数记为Gn=(an,bn,cn).小明发现:若G0=(4,8,18),则游戏永远无法结束,那么G2015=(9,10,11).分析 按照游戏规则,按照顺序操作找出数字变化规律,从G5开始3个一循环,进一步解决问题.
解答 解:若G0=(4,8,18),则G1=(5,9,16),G2=(6,10,14),G3=(7,11,12),G4=(8,12,10),
G5=(9,10,11),G6=(10,11,9),G7=(11,9,10),
G8=(9,10,11),G9=(10,11,9),G10=(11,9,10),…
由此看出从G5开始3个一循环,
(2015-4)÷3=670…1,
所以G2015与G5相同,也就是(9,10,11).
故答案为:(9,10,11).
点评 本题考查的是推理与论证,根据题意找出数字变化规律是解答此题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
3. 如图,AB是⊙O的直径,∠ABC=30°,OA=6,则扇形AOC面积为( )
如图,AB是⊙O的直径,∠ABC=30°,OA=6,则扇形AOC面积为( )
 如图,AB是⊙O的直径,∠ABC=30°,OA=6,则扇形AOC面积为( )
如图,AB是⊙O的直径,∠ABC=30°,OA=6,则扇形AOC面积为( )| A. | 2π | B. | 4π | C. | 6π | D. | 8π |
4.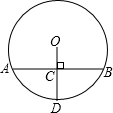 如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )
如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )
 如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )
如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )| A. | $\frac{25}{3}$cm | B. | 10cm | C. | 8cm | D. | $\frac{19}{3}$cm |
1.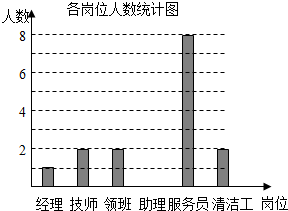 某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表
某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表
请回答下列问题:
(1)将各岗位人数统计图补充完整;
(2)求该公司服务员每人的基本工资;
(3)该公司所有员工基本工资的中位数是1500元,众数是1400元;你认为用基本工资的平均数和中位数来代表该公司员工基本工资的一般水平,哪一个更恰当?请说明理由.
(4)该公司一名员工向经理辞职了,若其他员工的基本工资不变,那么基本工资的平均数就降低了.你认为辞职的可能是哪个岗位上的员工呢?说明理由.
 某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表
某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表| 岗位 | 经理 | 技师 | 领班 | 助理 | 服务员 | 清洁工 |
| 基本工资 | 10000 | 4000 | 2400 | 1600 | 1000 |
(1)将各岗位人数统计图补充完整;
(2)求该公司服务员每人的基本工资;
(3)该公司所有员工基本工资的中位数是1500元,众数是1400元;你认为用基本工资的平均数和中位数来代表该公司员工基本工资的一般水平,哪一个更恰当?请说明理由.
(4)该公司一名员工向经理辞职了,若其他员工的基本工资不变,那么基本工资的平均数就降低了.你认为辞职的可能是哪个岗位上的员工呢?说明理由.
8.2015年,扬州中考考生约36000人,则数据36000用科学记数法表示为( )
| A. | 0.36×105 | B. | 3.6×103 | C. | 3.6×104 | D. | 3.6×105 |
18.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)3是方程ax2+(b-1)x+c=0的一个根;
(4)当x<-1或x>3时,ax2+(b-1)x+c<0.
其中正确的个数为( )
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)3是方程ax2+(b-1)x+c=0的一个根;
(4)当x<-1或x>3时,ax2+(b-1)x+c<0.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.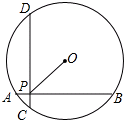 如图,在半径为5的圆中,AB、CD互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
如图,在半径为5的圆中,AB、CD互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
 如图,在半径为5的圆中,AB、CD互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
如图,在半径为5的圆中,AB、CD互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4 | D. | 3 |
2.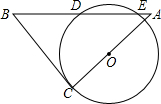 如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
 如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )| A. | 3cm | B. | $\frac{20}{7}$cm | C. | $\sqrt{10}$cm | D. | 2$\sqrt{2}$cm |
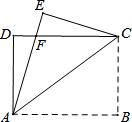 如图,四边形ABCD是矩形,AB=4cm,AD=3cm,把矩形沿直线AC折叠,点B落在点E处交DC于点F,则△ADF和△EFC的周长之和为14cm.
如图,四边形ABCD是矩形,AB=4cm,AD=3cm,把矩形沿直线AC折叠,点B落在点E处交DC于点F,则△ADF和△EFC的周长之和为14cm.