题目内容
14.化简$\frac{{a}^{2}}{a-b}$-$\frac{{b}^{2}}{a-b}$的结果是( )| A. | a+b | B. | a | C. | a-b | D. | b |
分析 原式利用同分母分式的减法法则计算,约分即可得到结果.
解答 解:原式=$\frac{{a}^{2}-{b}^{2}}{a-b}$
=$\frac{(a+b)(a-b)}{a-b}$
=a+b.
故选A.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 若$\frac{\sqrt{x-1}}{x-2}$有意义,则有x≥1且x≠2 | B. | 勾股定理是a2+b2=c2 | ||
| C. | 夹在两条平行线间的线段相等 | D. | a0=1 |
6.如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
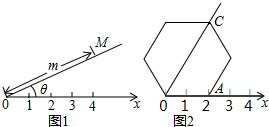

| A. | (60°,4) | B. | (45°,4) | C. | (60°,2) | D. | (50°,2) |
7.已知点A(2,-3),线段AB与坐标轴平行,则点B的坐标可能是( )
| A. | (-1,-2) | B. | (3,-2) | C. | (1,2) | D. | (-2,-3) |
 某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知骑自行车上学的学生有26人,则采用其他方式上学的学生人数为4 人.
某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知骑自行车上学的学生有26人,则采用其他方式上学的学生人数为4 人.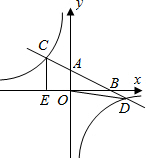 如图在平面直角坐标系xOy中,直线y1=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数y2=$\frac{k}{x}$(k≠0)的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
如图在平面直角坐标系xOy中,直线y1=-$\frac{1}{2}$x+2分别与x、y轴交于点B、A,与反比例函数y2=$\frac{k}{x}$(k≠0)的图象分别交于点C、D,CE⊥x轴于点E,OE=2.