题目内容
5. 如图.在△ABC中,AB=4,D是AB上一点(不与点A、B)重合,DE∥BC,交AC于点E.设△ABC的面积为S,△DEC的面积为S′.
如图.在△ABC中,AB=4,D是AB上一点(不与点A、B)重合,DE∥BC,交AC于点E.设△ABC的面积为S,△DEC的面积为S′.(1)当D是AB中点时,求$\frac{S′}{S}$的值;
(2)设AD=x,$\frac{S′}{S}$=y,求y与x的函数表达式,并写出自变量x的取值范围;
(3)根据y的范围,求S-4S′的最小值.
分析 (1)先求出△ADE和△CDE的面积相等,再根据平行线得出△ADE∽△ABC,推出$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{A{D}^{2}}{A{B}^{2}}$ 把AB=2AD代入求出即可;
(2)求出 $\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{16}$ x2①$\frac{{S}_{△ADE}}{{S}_{△DEC}}=\frac{AE}{EC}=\frac{x}{4-x}$ ②,联立①②即可求出函数关系式;y=$\frac{S'}{S}$=-$\frac{1}{16}$x2+$\frac{1}{4}$x,
(3)把函数关系式写成顶点式即可求出结论.
解答 解:(1)∵D为AB中点,
∴AB=2AD,
∵DE∥BC,
∴AE=EC,
∵△ADE的边AE上的高和△CED的边CE上的高相等,
∴S△ADE=S△CDE=S1,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=\frac{A{D}^{2}}{A{B}^{2}}=\frac{1}{4}$
∴S′:S=1:4;
(2)∵AB=4,AD=x,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=\frac{{x}^{2}}{16}$ ①,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{AE}{AC}$
∵AB=4,AD=x,∴$\frac{AE}{AC}=\frac{x}{4}$,∴$\frac{AE}{CE}=\frac{x}{4-x}$,∵△ADE的边AE上的高和△CED的边CE上的高相等,∴$\frac{{S}_{△ADE}}{{S}_{△DEC}}=\frac{AE}{EC}=\frac{x}{4-x}$ ②,
①÷②得:
∴y=$\frac{S'}{S}$=-$\frac{1}{16}$x2+$\frac{1}{4}$x,
∵AB=4,
∴x的取值范围是0<x<4;
(3)由(2)知x的取值范围是0<x<4,
∴y=$\frac{S'}{S}$=-$\frac{1}{16}$x2+$\frac{1}{4}$x=-$\frac{1}{16}$(x-2)2+$\frac{1}{4}$≤$\frac{1}{4}$,
∴S′≤$\frac{1}{4}$S.
∴S≥4S′,
∴S-4S'≥0,
∴S-4S′的最小值为0.
点评 本题主要考查了相似三角形的性质和判定,三角形的面积的计算方法,二次函数的最值问题,熟练掌握相似三角形的判定和性质定理是解题的关键.

| A. | k≥0 | B. | k≤1 | C. | 0≤k<1 | D. | 0<k≤1 |
| 应试者 | 笔试 | 面试 | 实际操作 |
| 甲 | 95 | 85 | 90 |
| 乙 | 90 | 95 | 85 |
| 丙 | 85 | 90 | 94 |
(2)这家公司将笔试、面试、实际操作三项成绩按照一定比例确定应试者的平均成绩,已知实际操作占50%,面试成绩所占百分比为x(x>0),从成绩看,如果甲要想被录取,求x的取值范围应为多少?
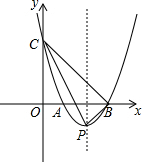 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于点A,B两点,且点B坐标为(3,0). 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径
 已知:如图,在正方形ABCD中,M,N分别是边AD,CD上的点,且∠MBN=45°,连接MN.求证:MN=AM+CN.
已知:如图,在正方形ABCD中,M,N分别是边AD,CD上的点,且∠MBN=45°,连接MN.求证:MN=AM+CN.