题目内容
2．
如图是边长为1的小正方形组成的格点图，坐标轴的单位长度为1，根据要求解答下列问题：（1）在图中作△A1B1C1，使它与△ABC关于y轴对称；
（2）若△PAC为等腰直角三角形，试写出所有满足条件点P的坐标：（0，2）、（-3，1）、（1，4）、（-5，2）、（-4，-1）、（2，1）．
分析 （1）直接利用轴对称的性质得出对应点位置进而得出答案；
（2）利用等腰直角三角形的性质得出符合题意的答案．
解答 
解：（1）如图所示：；
（2）当△PAC为等腰直角三角形，所有满足条件点P的坐标分别为：
（0，2）、（-3，1）、（1，4）、（-5，2）、（-4，-1）、（2，1）（写对一个得1分）．
故答案为：（0，2）、（-3，1）、（1，4）、（-5，2）、（-4，-1）、（2，1）．
点评 此题主要考查了轴对称变换以及等腰直角三角形的性质，得出所有符合题意的对应点是解题关键．
练习册系列答案
相关题目
12．
如图，已知平行四边形ABCD中，AC，BD相交于点O，AD=BD=8，AC=12，则△ADO的周长是（ ）
如图，已知平行四边形ABCD中，AC，BD相交于点O，AD=BD=8，AC=12，则△ADO的周长是（ ）| A． | 20 | B． | 18 | C． | 16 | D． | 12 |
13．下列各组数中，相等的是（ ）
| A． | （-3）2与-32 | B． | |-3|2与-32 | C． | （-3）3与-33 | D． | |-3|3与-33 |
如图，四边形ABCD内接于⊙O，AB为⊙O的直径，点C为$\widehat{BD}$的中点．若∠A=40°，求∠B的度数．
如图，在平面直角坐标系中
如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．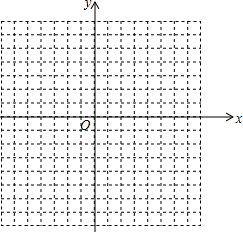
已知：抛物线C1：y=2x2+bx+6与抛物线C2关于y轴对称，抛物线C1与x轴分别交于点A（-3，0），B（m，0），顶点为M．
如图，在钝角△ABC中，∠B=20°，∠C=40°，AD是∠BAC的角平分线．