题目内容
10．
如图，四边形ABCD内接于⊙O，AB为⊙O的直径，点C为$\widehat{BD}$的中点．若∠A=40°，求∠B的度数．
分析 连接AC，根据圆周角定理求出∠ACB，根据圆心角、弧、弦的关系求出∠CAB，根据三角形内角和定理求出即可．
解答 解：连结AC，
∵AB是直径，
∴∠ACB=90°，
∵点C为$\widehat{BD}$的中点，∠DAB=40°，
∴∠BAC=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×40°=20°，
∴在Rt△ABC中，∠B=90°-20°=70°．
点评 本题考查了圆心角、弧、弦的关系，圆周角定理的应用，能正确作出辅助线是解此题的关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
如图，正方形的边长为4，以正方形中心为原点建立平面直角坐标系，作出函数y=$\frac{1}{3}$x2与y=-$\frac{1}{3}$x2的图象，则阴影部分的面积是8．
如图是边长为1的小正方形组成的格点图，坐标轴的单位长度为1，根据要求解答下列问题：
19．
已知抛物线y=-2x2+4x-1．
（1）该抛物线的对称轴是直线x=1，顶点坐标（1，1）；
（2）选取适当的数据填入下表，并在图中的直角坐标系内描点画出该抛物线的图象；
（3）若该抛物线上两点A（x1，y1），B（x2，y2）的横坐标满足
x1＜x2＜1，试比较y1与y2的大小．
已知抛物线y=-2x2+4x-1．（1）该抛物线的对称轴是直线x=1，顶点坐标（1，1）；
（2）选取适当的数据填入下表，并在图中的直角坐标系内描点画出该抛物线的图象；
| x | … | … | |||||
| y | … | … |
x1＜x2＜1，试比较y1与y2的大小．
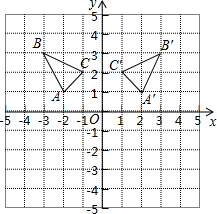如图是一个的正方形格纸，△ABC中A点坐标为（-2，1）．