题目内容
12. 如图,在钝角△ABC中,∠B=20°,∠C=40°,AD是∠BAC的角平分线.
如图,在钝角△ABC中,∠B=20°,∠C=40°,AD是∠BAC的角平分线.(1)画出AB边上的高CE(不要求尺规作图);
(2)延长CE交DA的延长线于点F,求∠EFA的度数.
分析 (1)首先画BA的延长线,再利用直角三角板一条直角边与AB重合,沿AB平移,使另一点过C,再画线即可;
(2)首先根据三角形内角和定理计算出∠BAC的度数,再根据角平分线定义可得∠BAD的度数,根据对顶角相等可得∠FAE的度数,然后可得∠EFA的度数.
解答 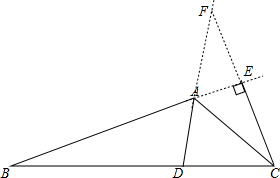 解:(1)如图所示:
解:(1)如图所示:
(2)在△ABC中,
∵∠B=20°,∠C=40°,
∴∠BAC=180°-∠B-∠ACB=120°,
又∵AD平分∠BAC,
∴∠BAD=$\frac{1}{2}$∠BAC=60°,
∴∠FAE=∠BAD=60°,
∴在Rt△FEA中,∠EFA=90°-∠FAE=30°.
点评 此题主要考查了复杂作图,以及角的计算,关键是掌握三角形高的画法,理清角之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在平面直角坐标系中,点A(-2,-3)在( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
1.一种面粉的质量标识为“28±0.25千克”,则下列面粉中合格的是( )
| A. | 28.30千克 | B. | 27.70千克 | C. | 28.51千克 | D. | 27.80千克 |
2.已知$\frac{x}{y}$=$\frac{3}{2}$,那么下列等式中一定正确的是( )
| A. | $\frac{3x}{y}$=$\frac{9}{2}$ | B. | $\frac{x+3}{y+3}$=$\frac{6}{5}$ | C. | $\frac{x-3}{y-2}$=$\frac{3}{2}$$•\frac{x}{y}$ | D. | $\frac{x+y}{x}$=$\frac{5}{2}$ |
 如图是边长为1的小正方形组成的格点图,坐标轴的单位长度为1,根据要求解答下列问题:
如图是边长为1的小正方形组成的格点图,坐标轴的单位长度为1,根据要求解答下列问题: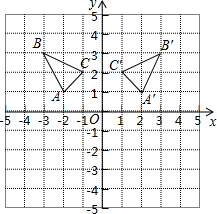 如图是一个的正方形格纸,△ABC中A点坐标为(-2,1).
如图是一个的正方形格纸,△ABC中A点坐标为(-2,1). 如图,在△ABC中,AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
如图,在△ABC中,AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.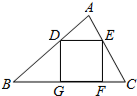 如图,△ABC中,点D、E是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形,若DE=2cm,求△ABC的面积.
如图,△ABC中,点D、E是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形,若DE=2cm,求△ABC的面积.