Question

6．如图，已知，∠BAC=90°，点D是直线BC上一点，DE⊥AB于点E，EF∥BC交AC于点F，设∠ACB=α
（1）当点D线段BC延长线上时，如图（1）求证：∠DEF=180°-α；
（2）当点D线段BC上时，如图（2）直接写出∠DEF与α的数量关系；
（3）在（1）的条件下，连接CE，当α=60°时，EC平分∠DEF，点G在直线CE上，且∠CAG=45°，求∠ACE的度数．

Answer 1

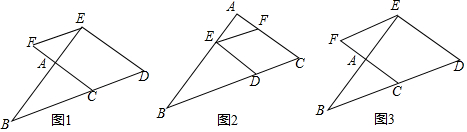
分析 （1）由DE⊥AB知∠DEA=∠CAB=90°，从而得AC∥DE即可知∠ACB=∠D=α，根据EF∥BC可得∠D+∠DEF=180°；
（2）由（1）知AC∥DE可得∠C=∠BDE=α，再根据EF∥BC可得；
（3）由AC∥DE知∠ACB=∠D=60°，根据EF∥BC得∠1=∠3、∠DEF=180°-∠D=120°，再由EC平分∠DEF得∠1=∠2=$\frac{1}{2}$∠DEF=60°，从而知∠3=∠2=60°，根据∠ACE=180°-∠ACB-∠3可得．

解答 解：（1）∵DE⊥AB，
∴∠DEA=∠CAB=90°，
∴AC∥DE，
∴∠ACB=∠D=α，
又∵EF∥BC，
∴∠D+∠DEF=180°，即∠DEF=180°-α；

（2）由（1）知，AC∥DE，
∴∠C=∠BDE=α，
又∵EF∥BC，
∴∠BDE=∠DEF=α；

（3）如图，连接CE，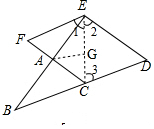

∵AC∥DE，
∴∠ACB=∠D=60°，
又∵EF∥BC，
∴∠1=∠3，∠DEF+∠D=180°，
∴∠DEF=180°-∠D=120°，
∵EC平分∠DEF，
∴∠1=∠2=$\frac{1}{2}$∠DEF=60°，
∴∠3=∠2=60°，
则∠ACE=180°-∠ACB-∠3=60°．

点评 本题主要考查平行线的判定与性质及角平分线的定义、垂直的性质，熟练掌握平行线的判定与性质是解题的关键．