题目内容
9.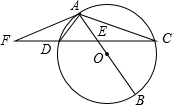 如图,已知AB是⊙O的直径,弦CD交AB于点E,作∠DAF=∠ACD,交CD延长线于点F.
如图,已知AB是⊙O的直径,弦CD交AB于点E,作∠DAF=∠ACD,交CD延长线于点F.(1)求证:AF为⊙O的切线;
(2)如果DE=DF,$\frac{DE}{CE}$=$\frac{3}{4}$,AC=8$\sqrt{5}$,求AE的长度.
分析 ①连接BD,根据圆周角性质即可证明∠BAF是直角,即可解题;
②连接BC,根据切线性质得出直角三角形,运用勾股定理即可解题;
解答 解:①连接BD,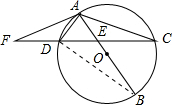
∵∠ABD和∠ACD都是$\widehat{AD}$对应的圆周角,
∴∠ABD=∠ACD,
∵AB是直径,∴∠ADB=90°,∴∠DAB+∠ABD=90°,
∴∠DAB+∠ACD=90°,
∵∠DAF=∠ACD,
∴∠DAB+∠DAF=90°,即∠BAF=90°,
∴AF为⊙O的切线;
②连接BC.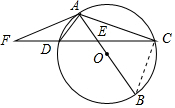
设CE=4x,AE=y,则DF=DE=3x,EF=6x
∵AB为⊙O的直径,AF为⊙O的切线,
∴∠EAF=90°,∠ACD=∠DAF.
又∵D为Rt△AEF的斜边EF的中点,
∴DA=DE=DF,
∴∠DAF=∠AFD,
∴∠ACD=∠AFD,
∴AF=AC=8$\sqrt{5}$.
在Rt△AEF中,由勾股定理得EF2=AE2+AF2,即36x2=y2+320.
设BE=z,由相交弦定理得CE•DE=AE•BE,即yz=4x•3x=12x2,
∴y2+320=3yz…①
又∵AD=DE,
∴∠DAE=∠AED.
又∵∠DAE=∠BCE,∠AED=∠BEC,
∴∠BCE=∠BEC,从而BC=BE=z.
在Rt△ACB中,由勾股定理得AB2=AC2+BC2,即(y+z)2=320+z2,
∴y2+2yz=320.…②
联立①②,解得y=8,z=16.
∴AE=8.
点评 解决本题的关键是作出辅助线找出直角三角形,考查了勾股定理、切线性质的运用.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
12.据报道,2016年10月17日7时30分28秒,神舟十一号载人飞船在甘肃酒泉发射升空,与天宫二号在距离地面393000米的太空轨道进行交会对接,而这也是未来我国空间站运行的轨道高度.393000用科学记数法表示为( )
| A. | 39.3×104 | B. | 3.93×105 | C. | 3.93×106 | D. | 0.393×106 |
18. 如图,在9×8的正方形的网格中,△ABC的三个顶点和点O都在格点上.
如图,在9×8的正方形的网格中,△ABC的三个顶点和点O都在格点上.
(1)画出△ABC关于直线l成轴对称△A1B1C;
(2)将△ABC以点A为旋转中心逆时针旋转90°,画出旋转后的△AB2C2.
 如图,在9×8的正方形的网格中,△ABC的三个顶点和点O都在格点上.
如图,在9×8的正方形的网格中,△ABC的三个顶点和点O都在格点上.(1)画出△ABC关于直线l成轴对称△A1B1C;
(2)将△ABC以点A为旋转中心逆时针旋转90°,画出旋转后的△AB2C2.
19.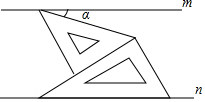 如图,在同一平面内,直线m∥n,将一副三角板按下列方式拼放在直线m与n之间,则含45°角的直角三角板斜边与直线m所夹锐角∠α的度数是( )
如图,在同一平面内,直线m∥n,将一副三角板按下列方式拼放在直线m与n之间,则含45°角的直角三角板斜边与直线m所夹锐角∠α的度数是( )
 如图,在同一平面内,直线m∥n,将一副三角板按下列方式拼放在直线m与n之间,则含45°角的直角三角板斜边与直线m所夹锐角∠α的度数是( )
如图,在同一平面内,直线m∥n,将一副三角板按下列方式拼放在直线m与n之间,则含45°角的直角三角板斜边与直线m所夹锐角∠α的度数是( )| A. | 10° | B. | 15° | C. | 25° | D. | 30° |
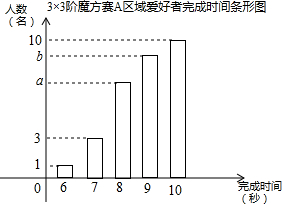 某次世界魔方大赛吸引世界各地共600名魔方爱好者参加,本次大赛首轮进行3×3阶魔方赛,组委会随机将爱好者平均分到20个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是3×3阶魔方赛A区域30名爱好者完成时间统计图,求:
某次世界魔方大赛吸引世界各地共600名魔方爱好者参加,本次大赛首轮进行3×3阶魔方赛,组委会随机将爱好者平均分到20个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是3×3阶魔方赛A区域30名爱好者完成时间统计图,求: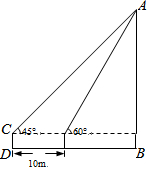 如图,为了测得一棵树的高度AB,小明在D处用高为1m的测角仪CD,测得树顶A的仰角为45°,再向树方向前进10m,又测得树顶A的仰角为60°,求这棵树的高度AB.
如图,为了测得一棵树的高度AB,小明在D处用高为1m的测角仪CD,测得树顶A的仰角为45°,再向树方向前进10m,又测得树顶A的仰角为60°,求这棵树的高度AB. 如图所示的⊙O中,若∠DBC=∠BAC=30°,则∠BDO=30°.
如图所示的⊙O中,若∠DBC=∠BAC=30°,则∠BDO=30°.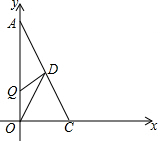 如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足$\sqrt{a-2b}$+|b-2|=0.
如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足$\sqrt{a-2b}$+|b-2|=0.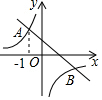 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$图象与一次函数y=kx+b的图象的2个交点分别为A(-1,n),B(2,n-3)
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$图象与一次函数y=kx+b的图象的2个交点分别为A(-1,n),B(2,n-3)