题目内容
14.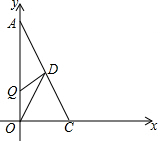 如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足$\sqrt{a-2b}$+|b-2|=0.
如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足$\sqrt{a-2b}$+|b-2|=0.(1)则C点的坐标为(2,0);A点的坐标为(0,4).
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.AC的中点D的坐标是(1,2),设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ?若存在,请求出t的值;若不存在,请说明理由.
分析 (1)直接利用绝对值的性质结合二次根式的定义分析得出a,b的值,进而得出答案;
(2)首先得出OP=2-t,QO=2t,D(1,2),再表示出△DOP和△DOQ的面积,进而得出等式求出答案.
解答 解:(1)∵$\sqrt{a-2b}$+|b-2|=0,
∴b-2=0,a-2b=0,
解得:b=2,a=4,
∴C(2,0),A(0,4);
故答案为:(2,0),(0,4);
(2)由题意可得:OP=2-t,QO=2t,D(1,2),
则S△DOP=$\frac{1}{2}$OP•yD=$\frac{1}{2}$(2-t)×2=2-t,
S△DOQ=$\frac{1}{2}$OQ•xD=$\frac{1}{2}$×2t×1=t,
∵S△ODP=S△ODQ,
∴2-t=t,
∴解得:t=1,
∴OP=1,QO=2,
∴P(1,0),Q(0,2).
点评 此题主要考查了三角形综合以及三角形面积表示方法,正确表示出OP,QO的长是解题关键.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
18. 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )
 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
19.x7可以表示为( )
| A. | x3+x4 | B. | x3•x4 | C. | x14÷x2 | D. | (x3)4 |
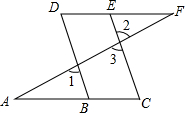 完成下列推理过程
完成下列推理过程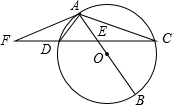 如图,已知AB是⊙O的直径,弦CD交AB于点E,作∠DAF=∠ACD,交CD延长线于点F.
如图,已知AB是⊙O的直径,弦CD交AB于点E,作∠DAF=∠ACD,交CD延长线于点F.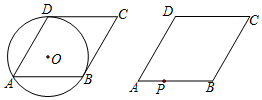
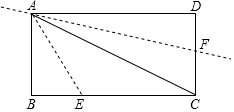 如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3$\sqrt{2}$,BC=3$\sqrt{6}$,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为2$\sqrt{3}$.
如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3$\sqrt{2}$,BC=3$\sqrt{6}$,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为2$\sqrt{3}$.