Question

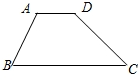已知一水坝的横断面是梯形ABCD，下底BC长14m，斜坡AB的坡度为3：

3

，另一腰CD与下底的交角为45°，且长为4

6

m，求它的上底的长（精确到0.1m）（

2

=1.414，

3

=1.732．）

Answer 1

考点：解直角三角形的应用-坡度坡角问题

专题：

分析：过点D作DF⊥BC，过点A作AE⊥BC，根据已知条件求出AE=DF的值，再根据坡度与特殊角的三角函数值求出BE，最后根据EF=BC-BE-FC，即可得出答案．

解答：解：过点D作DF⊥BC，过点A作AE⊥BC，
∵CD与BC的夹角为45°，
∴∠DCF=45°，
∴∠CDF=45°，
∵CD=4

6

，
∴DF=CF=

4 6

2

=4

3

，
∴AE=DF=4

3

，
∵斜坡AB的坡度为3：

3

，
∴tan∠ABE=

AE

BE

=

3

3

=

3

，
∴BE=4，
∵BC=14m，
∴EF=BC-BE-FC=14-4-4

3

10-4

3

，
∵AD=EF，
∴AD=10-4

3

≈3.1（m），
答：它的上底的长3.1m．

点评：此题考查了学生对坡度坡角的理解及梯形的性质的掌握情况．需注意构造直角三角形是常用的辅助线方法．