题目内容

已知a+b=5，ab=6，求a2+3ab+b2的值．
考点：完全平方公式
专题：
分析：将a2+3ab+b2转化为a2+2ab+b2+ab，然后将前三项结合利用完全平方公式转化为（a+b）2，然后将a+b=5，ab=6代入即可．
解答：解：a2+3ab+b2
=a2+2ab+b2+ab
=（a+b）2+ab．
当a+b=5，ab=6时，
原式=52+6=25+6=31．
点评：此题考查了完全平方公式及代入求值，解题的关键是将a2+3ab+b2转化为a2+2ab+b2+ab．
练习册系列答案
相关题目
已知等腰三角形其中两边的长分别是8和6，第三边的长是一元二次方程x2-16x+60=0的一个实数根，则该三角形的周长是（　　）
A、20B、24
C、24或20D、无法确定
用“＜”号或“＞”号填空：-7.6
 
-6.7．
点A（2，-7）到x轴的距离为
 
，到y轴的距离为
 
．
如图，∠B=∠C，∠A=∠D，下列结论：①AB∥CD；②AE∥DF；③AE⊥BC；④∠AMC=∠BND，其中正确的结论有（　　）
A、①②④B、②③④
C、③④D、①②③④
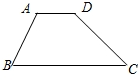已知一水坝的横断面是梯形ABCD，下底BC长14m，斜坡AB的坡度为3：
3
，另一腰CD与下底的交角为45°，且长为4
6
m，求它的上底的长（精确到0.1m）（
2
=1.414，
3
=1.732．）
若am=7，an=2，则am+n等于（　　）
A、9
B、5
C、14
D、
7
2
如果 a2-b2=10，a+b=3，则a-b=
 
．
若|2+a|+
3-b
=0，则a+b的值是（　　）
A、2B、0C、1D、-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网