题目内容
 △ABC中,∠C=90°,点D在边AB上,AD=AC=7,BD=
△ABC中,∠C=90°,点D在边AB上,AD=AC=7,BD=| 1 |
| 2 |
(1)求cosA的值.
(2)当以MN为直径的圆与△ABC一边相切时,求t的值.
考点:切线的性质,解直角三角形
专题:动点型
分析:(1)根据勾股定理求得BC的长度,即可得到cosA的值.
(2)分三种情况讨论:
当⊙O与AB相切时,则MN⊥AB,利用相似 AN:AM=AC:AB,得到比例式,即可求得答案;
当⊙O与AC相切时,则MN⊥AC,利用相似 AN:AM=AC:AB,得到比例式,即可求得答案;
当⊙O与BC相切时,作NE⊥BC,垂足为E,取EC的中点F,连结OF,易得△FCM∽△NEF.,利用比例求解即可
(2)分三种情况讨论:
当⊙O与AB相切时,则MN⊥AB,利用相似 AN:AM=AC:AB,得到比例式,即可求得答案;
当⊙O与AC相切时,则MN⊥AC,利用相似 AN:AM=AC:AB,得到比例式,即可求得答案;
当⊙O与BC相切时,作NE⊥BC,垂足为E,取EC的中点F,连结OF,易得△FCM∽△NEF.,利用比例求解即可
解答:解:(1)∵△ABC中,∠C=90°,AD=AC=7,BD=
BC.
∴(7+
BC)2=BC2+72,解得:BC=
,
∴BD=
,
∴AB=7+
=
,
∴cosA=
=
=
;
(2)当⊙O与AB相切时,则MN⊥AB,
∵∠MNA=∠C=90°∠A=∠MAN,
∴△MNA∽△BCA,
∴
=
,
即
=
,解得:t=2;
当⊙O与AC相切时,则MN⊥AC,
∵∠NMA=∠C=90°∠A=∠MAN,
∴△ANM∽△ABC,
∴
=
,
即
=
,解得:t=-14(舍去),
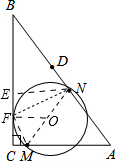
当⊙O与BC相切时,如图,作NE⊥BC,垂足为E.取EC的中点F,连结OF,则OF⊥BC,即点F为⊙O与BC相切的切点.
连结MF,NF,则FM⊥FN,因此△FCM∽△NEF.
因此CM•EN=EF2=FC2,
CM=t,EN=(
+2t)•
,EF=FC=
EC=
(7-2t),
因此t•(
+2t)•
=(
(7-2t))2,整理得t2+13t-14=0,解得:t=1,t=-14(舍去).
综上所得,当以MN为直径的圆与△ABC一边相切时,t=1或t=2.
| 1 |
| 2 |

∴(7+
| 1 |
| 2 |
| 28 |
| 3 |
∴BD=
| 14 |
| 3 |
∴AB=7+
| 14 |
| 3 |
| 35 |
| 3 |
∴cosA=
| AC |
| AB |
| 7 | ||
|
| 3 |
| 5 |
(2)当⊙O与AB相切时,则MN⊥AB,
∵∠MNA=∠C=90°∠A=∠MAN,
∴△MNA∽△BCA,
∴
| AM |
| AN |
| AB |
| AC |
即
| 7-t |
| 7-2t |
| 5 |
| 3 |
当⊙O与AC相切时,则MN⊥AC,
∵∠NMA=∠C=90°∠A=∠MAN,
∴△ANM∽△ABC,
∴
| AM |
| AN |
| AC |
| AB |
即
| 7-t |
| 7-2t |
| 3 |
| 5 |
当⊙O与BC相切时,如图,作NE⊥BC,垂足为E.取EC的中点F,连结OF,则OF⊥BC,即点F为⊙O与BC相切的切点.
连结MF,NF,则FM⊥FN,因此△FCM∽△NEF.
因此CM•EN=EF2=FC2,
CM=t,EN=(
| 4 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
因此t•(
| 4 |
| 3 |
| 3 |
| 5 |
| 2 |
| 5 |
综上所得,当以MN为直径的圆与△ABC一边相切时,t=1或t=2.

点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理和垂径定理,注意分类讨论是解题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,已知AB⊥DC于点B,AB=DB,点E在AB上,BE=BC,延长DE,交AC于点F,求证:DE=AC,DE⊥AC.
如图,已知AB⊥DC于点B,AB=DB,点E在AB上,BE=BC,延长DE,交AC于点F,求证:DE=AC,DE⊥AC.