题目内容
已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
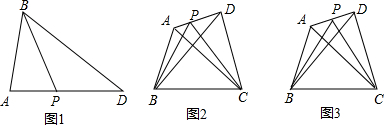
(1)当点C,E,F在直线AB的同侧(如图1所示)时,试说明∠BOE=2∠COF;
(2)当点C与点E,F在直线AB的两侧(如图2所示)时,(1)中结论是否仍然成立?请写出你的结论,并说明理由.

(1)当点C,E,F在直线AB的同侧(如图1所示)时,试说明∠BOE=2∠COF;
(2)当点C与点E,F在直线AB的两侧(如图2所示)时,(1)中结论是否仍然成立?请写出你的结论,并说明理由.

考点:角的计算,角平分线的定义
专题:
分析:(1)先设∠COF=x,得出∠EOF=90°-x,再根据角平分线的定义得出∠AOC=90°-2x,从而得出∠BOE=2∠COF的数量关系;
(2)根据(1)得出的∠BOE=2∠COF,∠AOF=∠EOF=x,得出∠AOC=90°-2x,再根据∠COE=90°,即可得出∠BOE与∠COF之间的关系.
(2)根据(1)得出的∠BOE=2∠COF,∠AOF=∠EOF=x,得出∠AOC=90°-2x,再根据∠COE=90°,即可得出∠BOE与∠COF之间的关系.
解答:解:(1)设∠COF=x,则∠EOF=90°-x,
∵OF平分∠AOE,
∴∠AOF=∠EOF,
∴∠AOC═∠AOF-∠COF=90°-2x,
∴∠BOE=90°-∠AOC=2x=2∠COF;
(2)∵∠BOE=2∠COF,∠AOF=∠EOF=x,则∠AOC=90°-2x,
∴∠COF=90°-x,
∴∠BOE=180°-∠AOE=180°-2x=2∠COF.
∵OF平分∠AOE,
∴∠AOF=∠EOF,
∴∠AOC═∠AOF-∠COF=90°-2x,
∴∠BOE=90°-∠AOC=2x=2∠COF;
(2)∵∠BOE=2∠COF,∠AOF=∠EOF=x,则∠AOC=90°-2x,
∴∠COF=90°-x,
∴∠BOE=180°-∠AOE=180°-2x=2∠COF.
点评:此题考查了角平分线的定义和角的计算,关键是根据角平分线的定义求出各角之间的数量关系.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
二次根式2
、
、
、
中,最简二次根式的个数是( )
| xy |
| 8 |
| x+y |
|
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,直线y=
如图,直线y=