题目内容
10.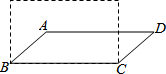 如图,若将4根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积变成矩形面积的一半,则这个平行四边形中∠ABC的度数为30°.
如图,若将4根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积变成矩形面积的一半,则这个平行四边形中∠ABC的度数为30°.
分析 作AE⊥BC于E,根据平行四边形的面积=矩形面积的一半,得出AE=$\frac{1}{2}$AB,再由三角函数即可求出∠ABC的度数.
解答 解:作AE⊥BC于E,如图所示: 则∠AEB=90°,
则∠AEB=90°,
根据题意得:平行四边形的面积=BC•AE=$\frac{1}{2}$BC•AB,
∴AE=$\frac{1}{2}$AB,
∴sin∠ABC=$\frac{AE}{AB}$=$\frac{1}{2}$,
∴∠ABC=30°.
故答案为:30°.
点评 本题考查了平行四边形的性质、矩形的性质、面积的计算以及三角函数;熟练掌握平行四边形和矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
20.下列二次根式中,是最简二次根式为( )
| A. | $\sqrt{27}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{{x^2}+{y^2}}$ | D. | $\sqrt{0.3x}$ |
5.如果圆锥的底面周长为20π,母线长为30,则该圆锥的侧面积为( )
| A. | 100π | B. | 200π | C. | 300π | D. | 400π |
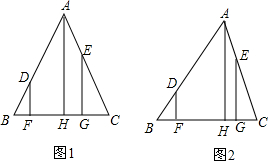 已知△ABC,点D,E分别在边AB,AC上,分别过A,D,E作BC的垂线,垂足为H,F,G.
已知△ABC,点D,E分别在边AB,AC上,分别过A,D,E作BC的垂线,垂足为H,F,G.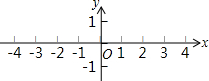 如图,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1),B(-4,1),C(-4,0).画出△ABC,并画出△ABC关于y轴对称的图形.
如图,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1),B(-4,1),C(-4,0).画出△ABC,并画出△ABC关于y轴对称的图形.