题目内容
1.已知平行四边形ABCD中,E为直线BC上一点,BC=3CE,连接AE,BD交于点F,则BF:FD=2:3或4:3.分析 根据题意画出图形,进而利用E在线段BC上或在BC的延长线上,进而求出答案.
解答  解:如图所示:∵平行四边形ABCD中,
解:如图所示:∵平行四边形ABCD中,
∴AD∥BC,AD=BC,
∴△BFE∽△DFA,
∴$\frac{BE}{AD}$=$\frac{BF}{DF}$,
∵BC=3CE,
∴BE=$\frac{2}{3}$BC,
∴$\frac{BF}{FD}$=$\frac{2}{3}$,
同理可得:△ADF′∽△E′BF′,
则$\frac{BF′}{DF′}$=$\frac{BE′}{AD}$,
故$\frac{BF′}{DF′}$=$\frac{4}{3}$,
故BF:FD=2:3或4:3.
故答案为:2:3或4:3.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质,正确分类讨论是解题关键.

练习册系列答案
相关题目
11.下列线段不能构成直角三角形的是( )
| A. | a=6,b=8,c=10 | B. | a=1,b=$\sqrt{2}$,c=$\sqrt{3}$ | C. | a=3,b=4,c=5 | D. | a=2,b=3,c=$\sqrt{6}$ |
13.下列各个实数中,无理数是( )
| A. | 2 | B. | 3.14 | C. | $\frac{7}{13}$ | D. | $\sqrt{2}$ |
11.-$\frac{3}{4}$的倒数是( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
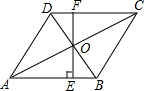 如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于F,则EF的长为( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于F,则EF的长为( ) 如图,已知平面直角坐标系中存在点M(2,0),点A(a,0).在x轴负半轴上有点C,且满足AM=OC,现以AC为对角线作正方形ABCD,设AM的中点为P,当以点O为圆心,OP为半径的圆与正方形ABCD的边相切时,a的值是2$\sqrt{2}$+2或6+4$\sqrt{2}$或6-4$\sqrt{2}$.
如图,已知平面直角坐标系中存在点M(2,0),点A(a,0).在x轴负半轴上有点C,且满足AM=OC,现以AC为对角线作正方形ABCD,设AM的中点为P,当以点O为圆心,OP为半径的圆与正方形ABCD的边相切时,a的值是2$\sqrt{2}$+2或6+4$\sqrt{2}$或6-4$\sqrt{2}$.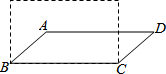 如图,若将4根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积变成矩形面积的一半,则这个平行四边形中∠ABC的度数为30°.
如图,若将4根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积变成矩形面积的一半,则这个平行四边形中∠ABC的度数为30°.