题目内容
3．矩形ABCD中，AD=8，AB=6，P，Q两点分别是边BC，CD上的动点，将△PCQ沿PQ翻折，C的对应点为E，连接DE，则当DE最小时，CQ的长为多少？分析 当P与B重合，折叠后C的对称点在BD上时，DE最小，根据折叠的性质CQ=QE，设CQ=x，根据勾股定理列方程求解即可．
解答 解：∵四边形ABCD是矩形，
∴CD=AB=6，BC=AD=8，∠C=90°，
∴BD=10，
∵当P与B重合，折叠后C的对称点在AB上时，DE最小．
∴BC=BE=8，EQ=CQ，
∴DE=10-8=2，
在Rt△DEQ中，设QE=x，则DQ=6-x，
∴（6-x）2=x2+22，
解得：x=$\frac{8}{3}$．
∴当DE最小时，CQ的长为$\frac{8}{3}$．
点评 本题考查了矩形的性质、折叠的性质、勾股定理；熟练掌握翻折变换和矩形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
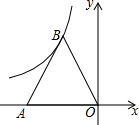如图，等边三角形AOB的顶点A的坐标为（-4，0），顶点B在反比例函数y=$\frac{k}{x}$（x＜0）的图象上，则k=-4$\sqrt{3}$．
已知：△ABC中，∠B=2∠C，AD⊥BC，E为BC的中点，求证：AB=2DE．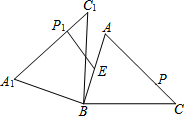
如图，在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1B1C1．点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，线段EP1长度的最小值是$\frac{5\sqrt{2}}{2}$-2．
15．某商店需要购进甲、乙两种商品共120件，其进价和售价如下表：（注：获利=售价-进价）
（1）若商店计划销售完这批商品后能获利1000元，请问甲、乙两种商品应分别购进多少件？
（2）若商店计划投入资金少于4000元，且销售完这批商品后获利多于1135元，请问有哪几种购货方案？并指出获利最大的购货方案．
| 甲 | 乙 | |
| 进价（元/件） | 15 | 35 |
| 售价（元/件） | 20 | 45 |
（2）若商店计划投入资金少于4000元，且销售完这批商品后获利多于1135元，请问有哪几种购货方案？并指出获利最大的购货方案．
