Question

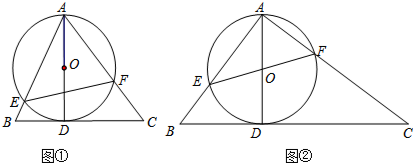
11．已知：△ABC中，∠B=2∠C，AD⊥BC，E为BC的中点，求证：AB=2DE．

Answer 1

分析 首先取AB中点F，连接FD，EF，判断出EF∥AC，即可判断出∠1=∠C，再根据∠B=2∠C，可得∠B=2∠1；然后根据AD⊥BC，AF=BF，判断出FD=BF=$\frac{1}{2}$AB；最后判断出∠1=∠3，即可判断出DF=DE，所以AB=2DE，据此解答即可．

解答 证明：如图，取AB中点F，连接FD，EF，，
∵AF=BF，BE=CE，
∴EF∥AC，
∴∠1=∠C，
∵∠B=2∠C，
∴∠B=2∠1，
∵AD⊥BC，AF=BF，
∴FD=BF=$\frac{1}{2}$AB，
∴∠B=∠2，
∴∠2=2∠1，
∵∠2=∠1+∠3，
∴∠1=∠3，
∴DF=DE，
∵FD=BF=$\frac{1}{2}$AB，
∴AB=2DE．

点评 （1）此题主要考查了三角形中位线定理的应用，要熟练掌握，解答此题的关键是要明确：三角形的中位线平行于第三边，并且等于第三边的一半．
（2）此题还考查了三角形的周长的含义和求法，要熟练掌握．