题目内容
15.某商店需要购进甲、乙两种商品共120件,其进价和售价如下表:(注:获利=售价-进价)| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(2)若商店计划投入资金少于4000元,且销售完这批商品后获利多于1135元,请问有哪几种购货方案?并指出获利最大的购货方案.
分析 (1)根据本题的等量关系甲件数+乙件数=120,甲总利润+乙总利润=1000,列出方程组,求解即可.
(2)设出所需未知数,根据甲进价×甲数量+乙进价×乙数量<4000;甲总利润+乙总利润>1135,列出不等式组,求解即可.
解答 解:设甲种商品应购进x件,乙种商品应购进y件.
根据题意得:$\left\{\begin{array}{l}{x+y=120}\\{5x+10y=1000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=80}\end{array}\right.$.
答:甲种商品购进40件,乙种商品购进80件.
(2)设甲种商品购进a件,则乙种商品购进(120-a)件.
根据题意得$\left\{\begin{array}{l}{15a+35(120-a)<4000}\\{5a+10(120-a)>1135}\end{array}\right.$,
解不等式组,得10<a<13.
∵a为非负整数,
∴a取11,12.
方案一:甲种商品购进11件,乙种商品购进109件.
方案二:甲种商品购进12件,乙种商品购进108件.
答:有两种购货方案,其中获利最大的是方案二.
点评 此题主要考查了二元一次方程组的应用以及一元一次不等式的应用,解决本题的关键是读懂题意,找到所求量的等量关系及符合题意的不等关系式组,求解即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
 二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )| A. | a<0 | B. | b>0 | C. | b2-4ac>0 | D. | a+b+c<0 |
10.长沙黄花国际机场进一步扩建,其建筑面积约26万平方米,将26万平方米用科学记数法表示为( )
| A. | 26×104平方米 | B. | 2.6×104平方米 | C. | 2.6×105平方米 | D. | 2.6×106平方米 |




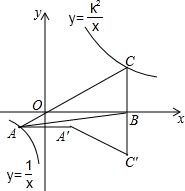 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}$(x>0,k是不等于0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,交于x轴于点B,连结AB,AA′,A′C′.若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于( )
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}$(x>0,k是不等于0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,交于x轴于点B,连结AB,AA′,A′C′.若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于( )