题目内容
如图，在△MBN中，BM=8，BN=6，点A，C，D分别是MB，NB，MN的中点，则平行四边形ABCD的周长是（ ）| A、16 | B、18 | C、14 | D、32 |
考点：三角形中位线定理,平行四边形的判定与性质
专题：
分析：由点A，C，D分别是MB，NB，MN的中点，根据中位线定理可知CD，AD是△MBN的中位线，故四边形ABCD的周长可求．
解答：解：如图，∵BM=8，BN=6，点A，C，D分别是MB，NB，MN的中点，
∴AD、CD是△BMN的中位线，
∴AD=
BN=3，CD=
MB=4，
∴平行四边形ABCD的周长是2（AD+CD）=14．
故选：C．
∴AD、CD是△BMN的中位线，
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴平行四边形ABCD的周长是2（AD+CD）=14．
故选：C．
点评：此题应根据三角形的中位线定理解答，三角形中位线性质应用比较广泛，尤其是在三角形、四边形方面起着非常重要作用．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
若（2x-3）2=4x2+2kx+9，则k的值为（ ）
| A、12 | B、-12 | C、6 | D、-6 |
下列运算正确的是（ ）
| A、-2（a-b）=-2a-2b |
| B、a2b-b2a=0 |
| C、3ab+2c=5abc |
| D、-2ab-（-3ab）=ab |
已知一个三角形的两个内角分别是30°，70°，另一个三角形的两个内角分别是70°，80°，则这两个三角形（ ）
| A、一定相似 | B、不一定相似 |
| C、一定不相似 | D、不能确定 |
若分式
的值为零，则x的值是（ ）
| x-1 |
| x+5 |
| A、0 | B、1 | C、-1 | D、-2 |
如果计算（x2-1）÷（x-1）的结果为0，则x的值是（ ）
| A、1 | B、-1 | C、0 | D、±1 |
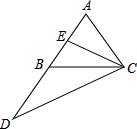在△ABC中，AD是BC边上的中线，延长AD到点E，使DE=AD，连结BE和CE，根据对角线互相平分的四边形是平行四边形，易得四边形ABEC是平行四边形．这种方法是数学证明常用的一种添辅助线的方法，叫做“加倍中线法”，请用这种方法解决下列问题：如图，在△ABC中，AB=AC，延长AB到点D，使DB=AB，E是AB的中点．求证：CD=2CE．