题目内容
已知一个三角形的两个内角分别是30°,70°,另一个三角形的两个内角分别是70°,80°,则这两个三角形( )
| A、一定相似 | B、不一定相似 |
| C、一定不相似 | D、不能确定 |
考点:相似三角形的判定
专题:
分析:根据三角形内角和定理求出另一个内角的度数,再根据有两组角对应相等的两个三角形相似即可作出判断.
解答:解:∵一个三角形的两个内角分别是30°,70°,
∴另一个内角的度数是180°-30°-70°=80°,
∵70°=70°,80°=80°,
∴这两个三角形一定相似.
故选:A.
∴另一个内角的度数是180°-30°-70°=80°,
∵70°=70°,80°=80°,
∴这两个三角形一定相似.
故选:A.
点评:考查了相似三角形的判定:
①平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;这是判定三角形相似的一种基本方法.相似的基本图形可分别记为“A”型和“X”型,如图所示在应用时要善于从复杂的图形中抽象出这些基本图形.
②三边法:三组对应边的比相等的两个三角形相似;
③两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
④两角法:有两组角对应相等的两个三角形相似.
①平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;这是判定三角形相似的一种基本方法.相似的基本图形可分别记为“A”型和“X”型,如图所示在应用时要善于从复杂的图形中抽象出这些基本图形.
②三边法:三组对应边的比相等的两个三角形相似;
③两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
④两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
相关题目
下列计算正确的是( )
| A、5a2-2a2=3 |
| B、2a+4a=6a2 |
| C、2y-3y=-1 |
| D、3m3n-m3n=2m3n |
(a2-b2)÷(a-b)的结果是( )
| A、a-b | B、a+b |
| C、-a+b | D、-a-b |
下列命题中,正确的是( )
| A、三角形的外心是三角形三条高线的交点 |
| B、等腰三角形的外心一定在它的内部 |
| C、任何一个三角形有且仅有一个外接圆 |
| D、三角形的内心可能在它的外部 |
 如图,在△MBN中,BM=8,BN=6,点A,C,D分别是MB,NB,MN的中点,则平行四边形ABCD的周长是( )
如图,在△MBN中,BM=8,BN=6,点A,C,D分别是MB,NB,MN的中点,则平行四边形ABCD的周长是( )| A、16 | B、18 | C、14 | D、32 |
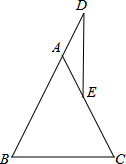 如图,在△ABC中,AB=AC,D为AC上任意一点,延长BA到点E,使得AE=AD,连接DE,求证:DE⊥BC.
如图,在△ABC中,AB=AC,D为AC上任意一点,延长BA到点E,使得AE=AD,连接DE,求证:DE⊥BC.