题目内容
11.已知2a2+2ab-18=0,求($\frac{{a}^{2}-{b}^{2}}{b}$)2÷(a2+ab)3×($\frac{ab}{b-a}$)2的值.分析 原式利用乘方的意义变形,约分得到最简结果,把已知等式变形后代入计算即可求出值.
解答 解:原式=$\frac{(a+b)^{2}(a-b)^{2}}{{b}^{2}}$•$\frac{1}{{a}^{3}(a+b)^{3}}$•$\frac{{a}^{2}{b}^{2}}{(a-b)^{2}}$=$\frac{1}{{a}^{2}+ab}$,
由2a2+2ab-18=0,得到a2+ab=9,
则原式=$\frac{1}{9}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.已知函数y=-$\frac{1}{2}$x+2,当-1<x≤1时,则y的取值范围( )
| A. | -$\frac{5}{2}$<y≤$\frac{3}{2}$ | B. | $\frac{3}{2}$<y<$\frac{5}{2}$ | C. | $\frac{3}{2}$<y≤$\frac{5}{2}$ | D. | $\frac{3}{2}$≤y<$\frac{5}{2}$ |
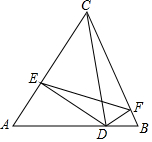 如图,在△ABC中,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F,求证:△CEF∽△CBA.
如图,在△ABC中,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F,求证:△CEF∽△CBA.