题目内容
20.已知函数y=-$\frac{1}{2}$x+2,当-1<x≤1时,则y的取值范围( )| A. | -$\frac{5}{2}$<y≤$\frac{3}{2}$ | B. | $\frac{3}{2}$<y<$\frac{5}{2}$ | C. | $\frac{3}{2}$<y≤$\frac{5}{2}$ | D. | $\frac{3}{2}$≤y<$\frac{5}{2}$ |
分析 分别求出x=-1,x=1时y的值,再根据一次函数的增减性即可求解.
解答 解:当x=-1时y=$\frac{1}{2}$+2=$\frac{5}{2}$,
当x=1时y=-$\frac{1}{2}$+2=$\frac{3}{2}$,
∵-$\frac{1}{2}$<0,
∴当-1<x≤1时,y的取值范围是$\frac{3}{2}$≤y<$\frac{5}{2}$.
故选:D.
点评 考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.

练习册系列答案
相关题目
10.关于多项式x5-3x2-7,下列说法正确的是( )
| A. | 最高次项是5 | B. | 二次项系数是3 | C. | 常数项是7 | D. | 是五次三项式 |
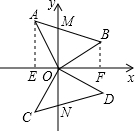 如图,在直角坐标系中,等腰直角△OAB的顶点与原点重合,△OCD与△OAB关于x轴对称,点C的对称点是A,点D的对称点是B,AB交y轴于点M,CD交y轴于点N.
如图,在直角坐标系中,等腰直角△OAB的顶点与原点重合,△OCD与△OAB关于x轴对称,点C的对称点是A,点D的对称点是B,AB交y轴于点M,CD交y轴于点N.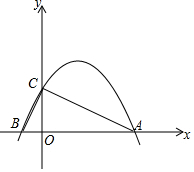 如图,抛物线y=ax2+bx+2交x轴于A、B两点,交y轴于点C,∠BCO=∠CAB,tan∠BCO=$\frac{1}{2}$
如图,抛物线y=ax2+bx+2交x轴于A、B两点,交y轴于点C,∠BCO=∠CAB,tan∠BCO=$\frac{1}{2}$