题目内容
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证:BC2=BD•BA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.

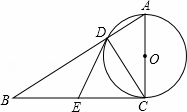
证明:(1)如图,连接OD.∵DE为切线,∴∠EDC+∠ODC=90°;
∵∠ACB=90°,∴∠ECD+∠OCD=90°.又∵OD=OC,∴∠ODC=∠OCD,
∴∠EDC=∠ECD,∴ED=EC;∵AC为直径,∴∠ADC=90°,
∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,∴∠B=∠BDE,∴ED=DB.
∴EB=EC,即点E为边BC的中点;
(2)∵AC为直径,∴∠ADC=∠ACB=90°,又∵∠B=∠B
∴△ABC∽△CDB,∴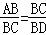 ,∴BC2=BD•BA;
,∴BC2=BD•BA;
(3)当四边形ODEC为正方形时,∠OCD=45°;∵AC为直径,
∴∠ADC=90°,∴∠CAD=∠ADC﹣∠OCD=90°﹣45°=45°
∴Rt△ABC为等腰直角三角形.

练习册系列答案
相关题目
 是关于
是关于 的方程
的方程 的一个根,则另一个根是………………( )
的一个根,则另一个根是………………( ) 1 B.
1 B.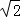 x+m=0,有两个不相等的实数根.
x+m=0,有两个不相等的实数根.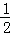 AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.
AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.
 与
与 ,其中
,其中 ,
, ,那么它们在同一坐标系中的图象可能是
,那么它们在同一坐标系中的图象可能是




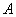 的坐标为(
的坐标为(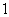 ,
,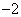 ),点
),点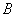 (3,
(3,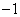 ),二次函数
),二次函数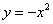 的图象为
的图象为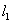 。
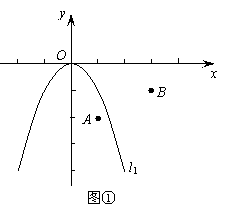
。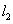 ,如图②,求抛物线
,如图②,求抛物线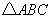 的面积;
的面积;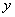 轴上是否存在点
轴上是否存在点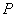 ,使
,使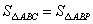 ,若存在,求出点
,若存在,求出点