题目内容
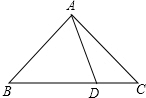 如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证:BD2+CD2=2AD2.
如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证:BD2+CD2=2AD2.考点:勾股定理
专题:证明题
分析:作AE⊥BC于E,由于∠BAC=90°,AB=AC,所以BE=CE,要证明BD2+CD2=2AD2,只需找出BD、CD、AD三者之间的关系即可,由勾股定理可得出AD2=AE2+ED2,AE2=AB2-BE2=AC2-CE2,ED=BD-BE=CE-CD,代入求出三者之间的关系即可得证.
解答: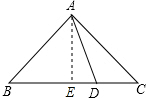 证明:作AE⊥BC于E,如图所示:
证明:作AE⊥BC于E,如图所示:
由题意得:ED=BD-BE=CE-CD,
∵在△ABC中,∠BAC=90°,AB=AC,
∴BE=CE=
BC,
由勾股定理可得:
AB2+AC2=BC2,
AE2=AB2-BE2=AC2-CE2,
AD2=AE2+ED2,
∴2AD2=2AE2+2ED2=AB2-BE2+(BD-BE)2+AC2-CE2+(CE-CD)2
=AB2+AC2+BD2+CD2-2BD×BE-2CD×CE
=AB2+AC2+BD2+CD2-2×
BC×BC
=BD2+CD2,即,BD2+CD2=2AD2.
 证明:作AE⊥BC于E,如图所示:
证明:作AE⊥BC于E,如图所示:由题意得:ED=BD-BE=CE-CD,
∵在△ABC中,∠BAC=90°,AB=AC,
∴BE=CE=
| 1 |
| 2 |
由勾股定理可得:
AB2+AC2=BC2,
AE2=AB2-BE2=AC2-CE2,
AD2=AE2+ED2,
∴2AD2=2AE2+2ED2=AB2-BE2+(BD-BE)2+AC2-CE2+(CE-CD)2
=AB2+AC2+BD2+CD2-2BD×BE-2CD×CE
=AB2+AC2+BD2+CD2-2×
| 1 |
| 2 |
=BD2+CD2,即,BD2+CD2=2AD2.
点评:本题考查的是勾股定理,关键在于找出直角三角形利用勾股定理求证,本题主要运用“等量代换”求出BD、CD、AD三者之间的关系.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列定理中有逆定理的是( )
| A、全等三角形对应角相等 |
| B、若a=0,则ab=0 |
| C、等腰三角形两腰上的高线相等 |
| D、负数的绝对值等于他的相反数 |
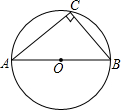 如图,△ABC内接于⊙O,AB为⊙O的直径,BC=6,AC=8.
如图,△ABC内接于⊙O,AB为⊙O的直径,BC=6,AC=8. 如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2-7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2-7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.