题目内容
 如图,锐角△ABC内接于⊙O,作BD⊥AC于点D.过圆心O作OM⊥AB于点M,已知cosC=
如图,锐角△ABC内接于⊙O,作BD⊥AC于点D.过圆心O作OM⊥AB于点M,已知cosC=| 2 |
| 7 |
考点:圆周角定理,垂径定理,解直角三角形
专题:
分析:连接AO并延长,交圆O于点N,连接BN,则OM是△ABN的中位线,根据圆周角定理即可得∠C=∠N,再由OM=1可得出BN的长,由cosC=
得出AN的长,进而可得出结论.
| 2 |
| 7 |
解答:
 解:连接AO并延长,交圆O于点N,连接BN.
解:连接AO并延长,交圆O于点N,连接BN.
∵AN是直径,
∴∠ABN=90°,
∵∠C与∠N是同弧所对的圆周角,
∴∠C=∠N,
∵OM⊥AB,点O是AN的中点,
∴OM是△ABN的中位线.
∴NB=2OM=2.
∵cosC=
,
∴
=
,即
=
,解得AN=7,
∴⊙O的半径=
.
故答案为:
.
 解:连接AO并延长,交圆O于点N,连接BN.
解:连接AO并延长,交圆O于点N,连接BN.∵AN是直径,
∴∠ABN=90°,
∵∠C与∠N是同弧所对的圆周角,
∴∠C=∠N,
∵OM⊥AB,点O是AN的中点,
∴OM是△ABN的中位线.
∴NB=2OM=2.
∵cosC=
| 2 |
| 7 |
∴
| NB |
| AN |
| 2 |
| 7 |
| 2 |
| AN |
| 2 |
| 7 |
∴⊙O的半径=
| 7 |
| 2 |
故答案为:
| 7 |
| 2 |
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
 如图,是一个几何体的三视图,则这个几何体的形状是( )
如图,是一个几何体的三视图,则这个几何体的形状是( )| A、圆柱 | B、圆锥 | C、圆台 | D、长方体 |
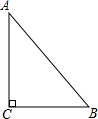 在Rt△ABC中∠C=90°,AB=6,sinA=
在Rt△ABC中∠C=90°,AB=6,sinA=| 2 |
| 3 |
| A、4 | ||||
B、2
| ||||
C、
| ||||
D、
|
 如图所示,已知AB∥CD,点E在直线AB上,射线EF交CD于点P,且∠FEB=50°,M为直线AB上一动点,射线MN过点P.
如图所示,已知AB∥CD,点E在直线AB上,射线EF交CD于点P,且∠FEB=50°,M为直线AB上一动点,射线MN过点P. 如图,在△ABC中,AB=AC=8,AB的垂直平分线DE分别交AB、AC于点E、D,BD=BC,△BCD的周长为13,求BC和ED的长.
如图,在△ABC中,AB=AC=8,AB的垂直平分线DE分别交AB、AC于点E、D,BD=BC,△BCD的周长为13,求BC和ED的长.