题目内容
16.从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=-$\frac{5}{2}$t2+10t(0≤t≤4).(1)当小球的高度是8.4m时,求此时小球的运动时间;
(2)求小球运动的最大高度.
分析 (1)当小球的高度是8.4m时,代入关系式是h=-$\frac{5}{2}$t2+10t(0≤t≤4)解方程即可;
(2)把函数关系式变形为顶点式,即可解决.
解答 解:(1)由题意可得,8.4=-$\frac{5}{2}$t2+10.
解得t1=1.2,t2=2.8.
∵0≤t≤4,
∴t1=1.2,t2=2.8都符合题意.
答:当小球的运动时间为1.2s或2.8s时,它的高度是8.4m.
(2)h=-$\frac{5}{2}$t2+10t=-$\frac{5}{2}$(t-2)2+10.
∵-$\frac{5}{2}$<0,
∴当小球的运动时间为2s时,小球运动的最大高度是10m.
点评 此题考查二次函数与一元二次方程的关系以及二次函数的实际应用,配方法求二次函数最值,把函数式化成顶点式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
 某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )| A. | 每月阅读数量的平均数是50 | B. | 众数是42 | ||
| C. | 中位数是58 | D. | 每月阅读数量超过40的有4个月 |
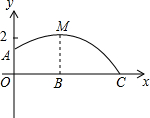 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.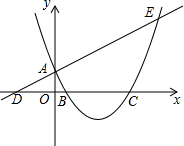 如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).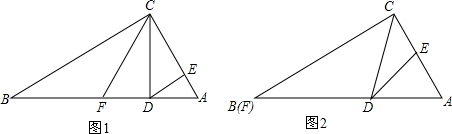
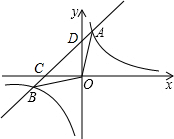 已知一次函数y1=kx+b与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.一次函数y1=kx+b与坐标轴交于C、D两点.求△AOB的面积.
已知一次函数y1=kx+b与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.一次函数y1=kx+b与坐标轴交于C、D两点.求△AOB的面积.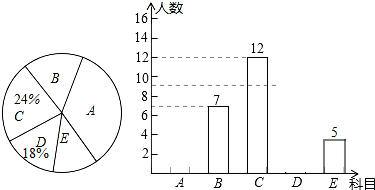
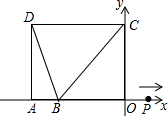 如图,在平面直角坐标系中,已知D (-5,4),B(-3,O),过点D分别作x轴、y轴的垂线,垂足分别为A、C两点,动点P从O点出发,沿x轴以每秒1个单位长度的速度向右运动,运动时间为t秒.
如图,在平面直角坐标系中,已知D (-5,4),B(-3,O),过点D分别作x轴、y轴的垂线,垂足分别为A、C两点,动点P从O点出发,沿x轴以每秒1个单位长度的速度向右运动,运动时间为t秒.