题目内容
根据下列条件求抛物线的解析式:
(1)图象过点(-1,-6)、(1,-2)和(0,3);
(2)图象的顶点坐标为(-1,-1),且与y轴交于点的纵坐标为-3;
(3)图象经过(1,0),(0,-3),且对称轴是直线x=2.
(1)图象过点(-1,-6)、(1,-2)和(0,3);
(2)图象的顶点坐标为(-1,-1),且与y轴交于点的纵坐标为-3;
(3)图象经过(1,0),(0,-3),且对称轴是直线x=2.
考点:待定系数法求二次函数解析式
专题:
分析:(1)设抛物线的解析式是y=ax2+bx+c,把(-1,-6)、(1,-2)和(0,3)代入得到一个三元一次方程组,求出方程组的解即可;
(2)根据抛物线的顶点坐标设抛物线的解析式是:y=a(x+1)2-1,把(0,-3)代入得到一个关于a的方程,求出a的值即可.
(3)已知抛物线的对称轴,可以设出函数的解析式是y=a(x-2)2+k,把(1,0),(0,-3)代入函数解析式即可求得函数解析式.
(2)根据抛物线的顶点坐标设抛物线的解析式是:y=a(x+1)2-1,把(0,-3)代入得到一个关于a的方程,求出a的值即可.
(3)已知抛物线的对称轴,可以设出函数的解析式是y=a(x-2)2+k,把(1,0),(0,-3)代入函数解析式即可求得函数解析式.
解答:解:(1)设抛物线的解析式是y=ax2+bx+c,
把(-1,-6)、(1,-2)和(0,3)代入得:
,
解得:
,
∴y=-7x2+2x+3
(2)设抛物线的解析式是:y=a(x+1)2-1,
把(0,-3)代入得:-3=a(0+1)2-1,
∴a=-2,
∴y=-2(x+1)2-1,即y=-2x2-4x-5.
(3)解:设函数的解析式是y=a(x-2)2+k,根据题意得:
,
解得:
,
则函数的解析式是y=-(x-2)2+1,即y=-x2+4x-3;
把(-1,-6)、(1,-2)和(0,3)代入得:
|
解得:
|
∴y=-7x2+2x+3
(2)设抛物线的解析式是:y=a(x+1)2-1,
把(0,-3)代入得:-3=a(0+1)2-1,
∴a=-2,
∴y=-2(x+1)2-1,即y=-2x2-4x-5.
(3)解:设函数的解析式是y=a(x-2)2+k,根据题意得:
|
解得:
|
则函数的解析式是y=-(x-2)2+1,即y=-x2+4x-3;
点评:本题考查了用待定系数法求出二次函数的解析式,解三元一次方程组,解一元一次方程等知识点的理解和掌握,关键是看学生如何正确地设抛物线的解析式,注意抛物线的解析式有:①三点式y=ax2+bx+c;②顶点式y=a(x-h)2+k,顶点坐标是(h,k);③交点式y=a(x-m)(x-n),抛物线与x轴的交点坐标是(m,0),(n,0).

练习册系列答案
相关题目
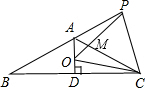 如图,等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP; ④S△ABC=S四边形AOCP,其中正确的有( )
如图,等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP; ④S△ABC=S四边形AOCP,其中正确的有( )| A、②③ | B、①②④ |
| C、③④ | D、①②③④ |
下列函数中,图象经过点(
,-4)的反比例函数是( )
| 1 |
| 2 |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
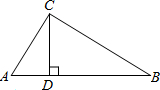 如图,直角三角形ABC,AC=3,BC=4,BA=5,CD是斜边AB上的高线,则CD=
如图,直角三角形ABC,AC=3,BC=4,BA=5,CD是斜边AB上的高线,则CD= 如图,AD是△ABC的中线,AB=
如图,AD是△ABC的中线,AB=