题目内容
如图1,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC.
(2)若AB=5,AD=3
,AE=3,求AF的长.
(3)在(2)的条件下,建立如图2所示的直角坐标系,在x轴上是否存在一点P,(P点不与B、C重合),使得由点P、A、E组成的三角形与△ABE相似?若存在,求出点P的坐标;若不存在,请说明理由.

(1)求证:△ADF∽△DEC.
(2)若AB=5,AD=3
| 3 |
(3)在(2)的条件下,建立如图2所示的直角坐标系,在x轴上是否存在一点P,(P点不与B、C重合),使得由点P、A、E组成的三角形与△ABE相似?若存在,求出点P的坐标;若不存在,请说明理由.

考点:相似形综合题
专题:
分析:(1)由平行四边形的性质可得到∠B+∠C=180°,而∠AFE+∠AFD=180°,结合条件可知∠AFD=∠C,由AD∥BC可得∠ADF=∠DEC,可证得△ADF∽△DEC;
(2)在Rt△ABE中可求得BE,则可求出EC,再利用(1)中相似可得到对应边成比例,代入可求得AF;
(3)设P点坐标为(x,0),则有△PAE∽△BAE或△PAE∽△ABE,再利用相似比得到关于x的方程,求出x并进行检验可得出点P的坐标.
(2)在Rt△ABE中可求得BE,则可求出EC,再利用(1)中相似可得到对应边成比例,代入可求得AF;
(3)设P点坐标为(x,0),则有△PAE∽△BAE或△PAE∽△ABE,再利用相似比得到关于x的方程,求出x并进行检验可得出点P的坐标.
解答:(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠ADF=∠DEC,∠B+∠C=180°,
∵∠AFE=∠B,
∴∠AFE+∠C=180°,且∠AFE+∠AFD=180°,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)解:∵AE⊥BC,
∴∠AEB=∠EAD=90°,AE=3,AD=3
在Rt△ADE中,可求得DE=6,
又∵四边形ABCD为平行四边形,∴CD=AB=5,
由(1)可知△ADF∽△DEC,
∴
=
,即
=
,
解得AF=
;
(3)解:假设存在满足条件P点,设其坐标为(x,0),则PE=|x|,
由(2)可知AB=5,AE=3,在Rt△ABE中可求得BE=4,
∵∠AEB=90°,
∴∠AEP=∠AEB=90°,
∴△ABE和△APE相似只能有两种情况,即△PAE∽△BAE或△PAE∽△ABE,
当△PAE∽△BAE时,则有
=
=1,即PE=BE,
∴|x|=4,解得x=4或x=-4(与B重合,舍去),此时P点坐标为(4,0);
当△PAE∽△ABE时,则有
=
,即
=
,可得|x|=
,解得x=
或x=-
,与B、C两点都不重合,
此时P点坐标为(
,0)或(-
,0);
综上可知存在使由点P、A、E组成的三角形与△ABE相似的点P,其坐标为(4,0)或(
,0)或(-
,0).
∴AB∥CD,AD∥BC,
∴∠ADF=∠DEC,∠B+∠C=180°,
∵∠AFE=∠B,
∴∠AFE+∠C=180°,且∠AFE+∠AFD=180°,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)解:∵AE⊥BC,
∴∠AEB=∠EAD=90°,AE=3,AD=3
| 3 |
在Rt△ADE中,可求得DE=6,
又∵四边形ABCD为平行四边形,∴CD=AB=5,
由(1)可知△ADF∽△DEC,
∴
| AF |
| CD |
| AD |
| DE |
| AF |
| 5 |
3
| ||
| 6 |
解得AF=
5
| ||
| 2 |
(3)解:假设存在满足条件P点,设其坐标为(x,0),则PE=|x|,
由(2)可知AB=5,AE=3,在Rt△ABE中可求得BE=4,
∵∠AEB=90°,
∴∠AEP=∠AEB=90°,
∴△ABE和△APE相似只能有两种情况,即△PAE∽△BAE或△PAE∽△ABE,
当△PAE∽△BAE时,则有
| PE |
| BE |
| AE |
| AE |
∴|x|=4,解得x=4或x=-4(与B重合,舍去),此时P点坐标为(4,0);
当△PAE∽△ABE时,则有
| PE |
| AE |
| AE |
| BE |
| |x| |
| 3 |
| 3 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
此时P点坐标为(
| 9 |
| 4 |
| 9 |
| 4 |
综上可知存在使由点P、A、E组成的三角形与△ABE相似的点P,其坐标为(4,0)或(
| 9 |
| 4 |
| 9 |
| 4 |
点评:本题主要考查相似三角形的判定和性质及下行四边形的性质、勾股定理等知识的综合应用,掌握相似三角形的判定方法是关键,注意角相等的寻找.在(3)中只知相似但没说对应关系,所以分两种情况讨论是解题的关键,注意利用线段长与点的坐标之间的关系.

练习册系列答案
相关题目
 如图,虚线部分是小刚作的辅助线,你认为线段CD( )
如图,虚线部分是小刚作的辅助线,你认为线段CD( )| A、是AC边上的高 |
| B、是BC边上的高 |
| C、是AB边上的高 |
| D、不是△ABC的高 |
将直线y=2x+4向下平移2个单位,所得到的直线相当于原直线( )得到.
| A、向左平移1个单位 |
| B、向左平移2个单位 |
| C、向右平移1个单位 |
| D、向右平移2个单位 |
二次函数y=2x2-4x+m的图象上有点A(2013,a),B (2014,b),关于a,b的大小关系,下列正确的是( )
| A、a>b |
| B、a<b |
| C、a=b |
| D、m的取值不确定,无法确定a,b的大小 |
圆内接四边形ABCD的四个内角之比可能是( )
| A、1:2:3:4 |
| B、1:3:4:5 |
| C、2:3:4:5 |
| D、2:3:5:4 |
若一次函数y=kx+3的图象过点P(2,-1),则k的值( )
| A、2 | B、-2 | C、3 | D、-3 |
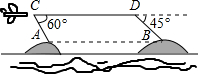 某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得你正前方一海岛顶端A的俯角是60°,然后沿平行与AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是45°,求两海岛间的距离AB.
某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得你正前方一海岛顶端A的俯角是60°,然后沿平行与AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是45°,求两海岛间的距离AB.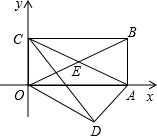 如图,把矩形纸片OABC放入直角坐标系中,是OA、OC分别落在x轴、y轴的正半轴上,连接AC将△ABC翻折,点B落在该坐标系平面内.设这个落点为点D,CD交x轴于E,已知CB=4,AB=2.
如图,把矩形纸片OABC放入直角坐标系中,是OA、OC分别落在x轴、y轴的正半轴上,连接AC将△ABC翻折,点B落在该坐标系平面内.设这个落点为点D,CD交x轴于E,已知CB=4,AB=2.