题目内容
 如图,AD是△ABC的中线,AB=
如图,AD是△ABC的中线,AB=| 37 |
考点:解直角三角形
专题:
分析:过A作AE⊥BC于点E,在Rt△ADE中可求得AE和DE,在Rt△ABE中可求得BE,可求出BD,则可求得CE,在Rt△AEC中可求得tan∠C.
解答: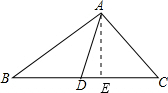 解:如图,过A作AE⊥BC于点E,
解:如图,过A作AE⊥BC于点E,
∵AD=4,∠ADC=60°,
∴DE=
AD=2,AE=
AD=2
,
在Rt△ABE中,AB=
,由勾股定理可求得BE=5,
∴BD=BE-DE=5-2=3,
∵AD为中线,
∴CD=BD=3,
∴CE=CD-DE=3-2=1,
在Rt△AEC中,tan∠C=
=
=2
.
 解:如图,过A作AE⊥BC于点E,
解:如图,过A作AE⊥BC于点E,∵AD=4,∠ADC=60°,
∴DE=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
在Rt△ABE中,AB=
| 37 |
∴BD=BE-DE=5-2=3,
∵AD为中线,
∴CD=BD=3,
∴CE=CD-DE=3-2=1,
在Rt△AEC中,tan∠C=
| AE |
| EC |
2
| ||
| 1 |
| 3 |
点评:本题主要考查三角函数的定义,掌握特殊角的三角函数和三角函数的定义是解题的关键.注意勾股定理的应用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
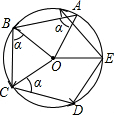 如图所示,小范从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小范第五次走到场地边缘时处于弧AB上,此时∠AOE=48°,则α的度数是( )
如图所示,小范从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小范第五次走到场地边缘时处于弧AB上,此时∠AOE=48°,则α的度数是( )| A、60° | B、51° |
| C、48° | D、76° |
 如图,虚线部分是小刚作的辅助线,你认为线段CD( )
如图,虚线部分是小刚作的辅助线,你认为线段CD( )| A、是AC边上的高 |
| B、是BC边上的高 |
| C、是AB边上的高 |
| D、不是△ABC的高 |
圆内接四边形ABCD的四个内角之比可能是( )
| A、1:2:3:4 |
| B、1:3:4:5 |
| C、2:3:4:5 |
| D、2:3:5:4 |
 在如图的三角形中,用三角尺或量角器过点A作BC的垂线,过点B作AC的垂线,过点C作AB的垂线.
在如图的三角形中,用三角尺或量角器过点A作BC的垂线,过点B作AC的垂线,过点C作AB的垂线.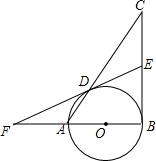 如图,在△ABC中,∠ABC=90°,AB=4,BC=5,以AB为直径的⊙O交AC于点D,点E是BC的中点,连接ED并延长交BA的延长线于点F.
如图,在△ABC中,∠ABC=90°,AB=4,BC=5,以AB为直径的⊙O交AC于点D,点E是BC的中点,连接ED并延长交BA的延长线于点F.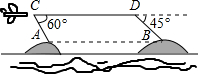 某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得你正前方一海岛顶端A的俯角是60°,然后沿平行与AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是45°,求两海岛间的距离AB.
某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得你正前方一海岛顶端A的俯角是60°,然后沿平行与AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是45°,求两海岛间的距离AB.