��Ŀ����
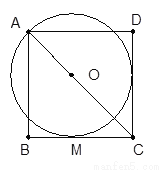
��ͼ��OΪ������ABCD�Խ�����һ�㣬��OΪԲ�ģ�OA��Ϊ�뾶�ġ�O��BC�����ڵ�M��
��1����֤��CD���O����;
��2����������ABCD�ı߳�Ϊ1�����O�İ뾶��
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ��OΪ������ABCD�Խ�����һ�㣬��OΪԲ�ģ�OA��Ϊ�뾶�ġ�O��BC�����ڵ�M��
��1����֤��CD���O����;
��2����������ABCD�ı߳�Ϊ1�����O�İ뾶��
