题目内容
5.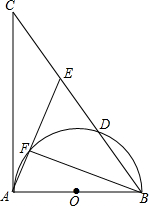 如图,在Rt△ABC中,∠BAC=90°,以AB为直径的半圆O交BC边于点D,点E在BC边上,且AE=AB,连结AE交半圆O于点F,连结BF.
如图,在Rt△ABC中,∠BAC=90°,以AB为直径的半圆O交BC边于点D,点E在BC边上,且AE=AB,连结AE交半圆O于点F,连结BF.(1)求证:∠C=∠EBF.
(2)若AF=4,$\frac{AB}{AC}=\frac{2}{3}$,求半圆O的直径.
分析 (1)根据余角的性质得到∠CAE=∠ABF,根据等腰三角形的性质得到∠ABE=∠AEB,于是得到∠C=∠EBF;
(2)解根据相似三角形的性质得到$\frac{EF}{BF}$=$\frac{AB}{AC}$=$\frac{2}{3}$,设EF=2x,BF=3x,求得AB=AE=4+2x,根据勾股定理即可得到结论.
解答 (1)证明:∵∠BAC=90°,
∴∠CAE+∠BAF=90°,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠FAB+∠ABF=90°,
∴∠CAE=∠ABF,
∵AE=AB,
∴∠ABE=∠AEB,
∵∠C=∠AEB-∠CAE,∠EBF=∠ABE-∠ABF,
∴∠C=∠EBF;
(2)解:∵∠C=∠EBF,∠BAC=∠EFB=90°,
∴△BAC∽△EFB,
∴$\frac{EF}{BF}$=$\frac{AB}{AC}$=$\frac{2}{3}$,
设EF=2x,BF=3x,
∴AB=AE=4+2x,
∵AB2=AF2+BF2,
∴(4+2x)2=(3x)2+42,
∴x=$\frac{16}{5}$,
∴AB=$\frac{52}{5}$,
∴半圆O的直径是$\frac{52}{5}$.
点评 本题考查了相似三角形的判定和性质,勾股定理,等腰三角形的性质,圆周角定理,掌握的识别图形是解题的关键.

练习册系列答案
相关题目
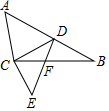 如图,△ABC中,∠ACB=90°,D为AB上一点,CE⊥CD,且$\frac{CD}{CB}$=$\frac{3}{5}$,$\frac{CE}{AC}$=$\frac{3}{5}$.求证:△ACD∽△ECF.
如图,△ABC中,∠ACB=90°,D为AB上一点,CE⊥CD,且$\frac{CD}{CB}$=$\frac{3}{5}$,$\frac{CE}{AC}$=$\frac{3}{5}$.求证:△ACD∽△ECF.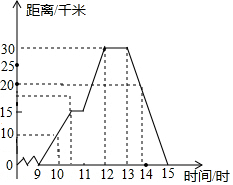 如图表示一人骑自行车离家的距离与时间的关系,骑车者9时离开家,15时到家,根据图象回答问题:
如图表示一人骑自行车离家的距离与时间的关系,骑车者9时离开家,15时到家,根据图象回答问题: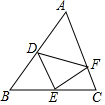 如图,设△ABC的面积为1,点D,E,F分别在AB,BC,CA上,AD=$\frac{1}{m}$AB,BE=$\frac{1}{n}$BC,CF=$\frac{1}{p}$CA,且满足m+n+p=9,m2+n2+p2=29.m3+n3+p3=99,求△DEF的面积.
如图,设△ABC的面积为1,点D,E,F分别在AB,BC,CA上,AD=$\frac{1}{m}$AB,BE=$\frac{1}{n}$BC,CF=$\frac{1}{p}$CA,且满足m+n+p=9,m2+n2+p2=29.m3+n3+p3=99,求△DEF的面积.