题目内容
15.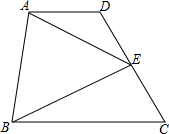 如图,E是梯形ABCD的腰DC的中点,证明:S△ABE=$\frac{1}{2}$S梯形ABCD.
如图,E是梯形ABCD的腰DC的中点,证明:S△ABE=$\frac{1}{2}$S梯形ABCD.
分析 作EF∥BC交AB于F,过F作梯形ABCD的高MN;先证明EF是梯形ABCD的中位线,得出EF=$\frac{1}{2}$(AD+BC),再求出△ABE的面积=△AEF的面积+△BEF的面积=$\frac{1}{2}$EF•MN,即可得出结论.
解答 解:作EF∥BC交AB于F,过F作梯形ABCD的高MN,如图所示: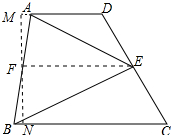 ∵E是梯形ABCD的腰DC的中点,
∵E是梯形ABCD的腰DC的中点,
∴EF是梯形ABCD的中位线,
∴EF=$\frac{1}{2}$(AD+BC),
∵△ABE的面积=△AEF的面积+△BEF的面积=$\frac{1}{2}$EF(MF+NF)=$\frac{1}{2}$EF•MN,
梯形ABCD的面积=$\frac{1}{2}$(AD+BC)•MN=EF•MN,
∴S△ABE=$\frac{1}{2}$S梯形ABCD.
点评 本题考查了梯形的性质、梯形中位线定理以及三角形面积和梯形面积的计算;运用梯形中位线定理得出面积关系是解决问题的关键.

练习册系列答案
相关题目
5.函数y=$\sqrt{x-2}$中自变量x的取值范围是( )
| A. | x≤2 | B. | x≥2 | C. | x<2 | D. | x>2 |
3.下列语句中,假命题的是( )
| A. | 相等的两个角是对顶角 | B. | 如果b∥a,c∥a,那么b∥c | ||
| C. | 两直线平行,同旁内角互补 | D. | 邻补角互补 |
13.在2,-$\sqrt{3}$,0,π这四个数中,最小的一个数是( )
| A. | -$\sqrt{3}$ | B. | 0 | C. | 2 | D. | π |
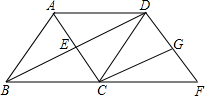 已知菱形ABCD的对角线AC与BD相交于点E,点F在BC的延长线上,且CF=BC,连接DF,点G是DF中点,连接CG.求证:四边形ECGD是矩形.
已知菱形ABCD的对角线AC与BD相交于点E,点F在BC的延长线上,且CF=BC,连接DF,点G是DF中点,连接CG.求证:四边形ECGD是矩形.