题目内容
6. 阅读材料,如图,在平面直角坐标系中,O为坐标原点,对于任意两点A(x1,y1),B(x2,y2).由勾股定理可得:AB2=(x1-x2)2+(y1-y2)2,我们把$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$叫做A,B两点之间的距离,记作AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
阅读材料,如图,在平面直角坐标系中,O为坐标原点,对于任意两点A(x1,y1),B(x2,y2).由勾股定理可得:AB2=(x1-x2)2+(y1-y2)2,我们把$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$叫做A,B两点之间的距离,记作AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$在平面直角坐标系中,O为坐标原点,设点P(x,0),已知A(0,2),B(3,-2),则AB=5,PA=$\sqrt{{x}^{2}+4}$.
分析 直接利用两点间的距离公式计算即可.
解答 解:∵A(0,2),B(3,-2),
∴AB=$\sqrt{(3-0)^{2}+(-2-2)^{2}}$=5,
∵P(x,0),A(0,2),
∴PA=$\sqrt{(x-0)^{2}+(0-2)^{2}}$=$\sqrt{{x}^{2}+4}$.
故答案为5,$\sqrt{{x}^{2}+4}$.
点评 本题考查了两点间的距离公式:对于任意两点A(x1,y1),B(x2,y2),则AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.某户家庭去年收支和结余与前年相比,总收入增长了20%,总支出增长了15%,结余增加了0.75万元,设前年总收入为x万元,总支出为y万元.填表:
| 总收入/万元 | 总支出/万元 | 结余/万元 | |
| 前年 | x | y | x-y |
| 去年 | 1.2x | 1.15y | 1.2x-1.15y |
11. 如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
 如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2}{3}$ |




 已知△ABC中,CD平分∠ACB,AQ⊥CD,P为AB的中点,求证:PQ=$\frac{1}{2}$(BC-AC)
已知△ABC中,CD平分∠ACB,AQ⊥CD,P为AB的中点,求证:PQ=$\frac{1}{2}$(BC-AC)
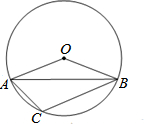 如图,在⊙O中,已知∠OAB=21.5°,则∠C的度数为111.5°.
如图,在⊙O中,已知∠OAB=21.5°,则∠C的度数为111.5°. 已知反比例函数y=$\frac{3-m}{x}$的图象如图所示,则实数m的取值范围在数轴上应表示为( )
已知反比例函数y=$\frac{3-m}{x}$的图象如图所示,则实数m的取值范围在数轴上应表示为( )


