题目内容
14.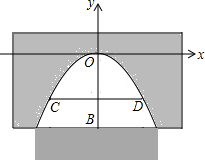 有一座抛物线形拱桥,正常水位时桥下的水深2m,拱顶距水面的距离OB=4m,在如图所示的直角坐标系中,该抛物线的解析式为y=-$\frac{1}{25}$x2,为保证过往船只顺利航行,桥下水面宽度不得小于18m(即CD的长),求水深超过多少米时就会影响过往船只在桥下顺利航行?
有一座抛物线形拱桥,正常水位时桥下的水深2m,拱顶距水面的距离OB=4m,在如图所示的直角坐标系中,该抛物线的解析式为y=-$\frac{1}{25}$x2,为保证过往船只顺利航行,桥下水面宽度不得小于18m(即CD的长),求水深超过多少米时就会影响过往船只在桥下顺利航行?
分析 把点(9,0)代入y=-$\frac{1}{25}$x2中的函数解析式就可以解决.
解答 解:当桥下水面的宽度等于18m时,抛物线上第四象限点的横坐标为9,
把x=9代入函数解析式y=-$\frac{1}{25}$x2中,
∴y=-$\frac{1}{25}$×92=-$\frac{81}{25}$(米),
∴4+2-$\frac{81}{25}$=$\frac{69}{25}$.
答:当水深超过$\frac{69}{25}$米时,超过了正常水位$\frac{19}{25}$米,就会影响过往船只在桥下顺利航行.
点评 本题考查利用图象上的点解决实际问题,正确理解题意是解决问题的关键.

练习册系列答案
相关题目
2.若将分式$\frac{a+b}{4ab}$中的a与b的值都扩大为原来的2倍,则这个分式的值将( )
| A. | 缩小为原来的$\frac{1}{2}$ | B. | 缩小为原来的$\frac{1}{4}$ | C. | 分式的值不变 | D. | 扩大为原来的2倍 |
19.下列一元二次方程中,有两个相等实数根的是( )
| A. | x2-8=0 | B. | 2x2-4x+3=0 | C. | 9x2+6x+1=0 | D. | 5x+2=3x2 |
3.2015年5月31日,我国飞人苏炳添在美国尤金举行的国际田联钻石联赛100米男子比赛中,获得好成绩,成为历史上首位突破10秒大关的黄种人.如表是苏炳添近五次大赛参赛情况:
则苏炳添这五次比赛成绩的众数和平均数分别为( )
| 比赛日期 | 2012-8-4 | 2013-5-21 | 2014-9-28 | 2015-5-20 | 2015-5-31 |
| 比赛地点 | 英国伦敦 | 中国北京 | 韩国仁川 | 中国北京 | 美国尤金 |
| 成绩(秒) | 10.19 | 10.06 | 10.10 | 10.06 | 9.99 |
| A. | 10.06秒,10.06秒 | B. | 10.10秒,10.06秒 | C. | 10.06秒,10.08秒 | D. | 10.08秒,10.06秒 |
 已知:如图,在平行四边形ABCD中,E,F分别是AB,CD上的两点,且AE=CF,AF、DE相交于点N,BF、CE相交于点M.求证:四边形EMFN是平行四边形.
已知:如图,在平行四边形ABCD中,E,F分别是AB,CD上的两点,且AE=CF,AF、DE相交于点N,BF、CE相交于点M.求证:四边形EMFN是平行四边形.