题目内容
 如图,?ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),顶点C,D在双曲线y=
如图,?ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),顶点C,D在双曲线y=| k |
| x |
| A、24 | B、27 | C、28 | D、32 |
考点:平行四边形的性质,反比例函数图象上点的坐标特征
专题:
分析:分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=1,由此设D(3,
),C(4,
),再由四边形ABCD是平行四边形可知两条对角线相交于一点,则其交点纵坐标相同,由此即可得出k的值.
| k |
| 3 |
| k |
| 4 |
解答: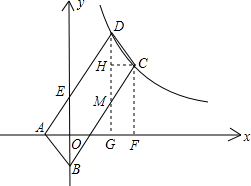 解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(ASA),
∴CH=AO=1,则C的横坐标是3.
∴设C(4,
),D(3,
),
∵四边形ABCD是平行四边形,
∵A(-1,0),B(0,-2),
∴k=24.
故选A.
 解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(ASA),
∴CH=AO=1,则C的横坐标是3.
∴设C(4,
| k |
| 4 |
| k |
| 2 |
∵四边形ABCD是平行四边形,
∵A(-1,0),B(0,-2),
∴k=24.
故选A.
点评:本题考查的是反比例函数综合题,涉及到全等三角形的判定与性质、反比例函数的性质等知识,比较复杂.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
(-3)2013×(
)2014等于( )
| 1 |
| 3 |
| A、-3 | ||
| B、3 | ||
C、-
|
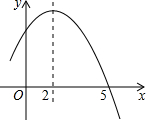 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c≥0的解集是( )
如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c≥0的解集是( )| A、-1≤x≤5 |
| B、x≥5 |
| C、x≤-1 |
| D、x≤-1或x≥5 |
 如图,在12×12正方形网格中作图:
如图,在12×12正方形网格中作图: 如图,若要得到DE∥BC,则需要条件
如图,若要得到DE∥BC,则需要条件 如图是两个半径都是4cm的圆,其中一个可以看作是由另一个圆平移得到,则平移的距离是
如图是两个半径都是4cm的圆,其中一个可以看作是由另一个圆平移得到,则平移的距离是 在直角坐标系中,⊙P、⊙Q的位置如图所示.在⊙P上且在⊙Q内部的格点坐标是
在直角坐标系中,⊙P、⊙Q的位置如图所示.在⊙P上且在⊙Q内部的格点坐标是 如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F,若BE=2,则CF长为
如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F,若BE=2,则CF长为