题目内容
 如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F,若BE=2,则CF长为
如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F,若BE=2,则CF长为考点:正方形的性质,角平分线的性质,等腰直角三角形
专题:
分析:根据正方形性质得出∠B=90°,∠ACB=45°,根据角平分线性质求出EF=BE,求出∠FEC=∠FCE=45°,推出EF=CF=BE,即可得出答案.
解答:证明:∵四边形ABCD是正方形,
∴∠B=90°,∠ACB=
∠DCB=45°,
∵AE平分∠BAC,EF⊥AC,
∴BE=EF,
∵EF⊥AC,
∴∠EFC=90°,
∵∠ACB=45°,
∴∠FEC=45°=∠FCE,
∴EF=FC=BE=2.
故答案为:2.
∴∠B=90°,∠ACB=
| 1 |
| 2 |
∵AE平分∠BAC,EF⊥AC,
∴BE=EF,
∵EF⊥AC,
∴∠EFC=90°,
∵∠ACB=45°,
∴∠FEC=45°=∠FCE,
∴EF=FC=BE=2.
故答案为:2.
点评:此题考查正方形的性质、角平分线性质,能综合运用性质进行推理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在平行四边形ABCD中,对角线AC、BD交于O点,过O点作直线交AD于E,交BC于F,图中能够全等的三角形共有( )
如图所示,在平行四边形ABCD中,对角线AC、BD交于O点,过O点作直线交AD于E,交BC于F,图中能够全等的三角形共有( )| A、2对 | B、4对 | C、6对 | D、8对 |
 如图所示,△ABC中,AC=5,中线AD=7,△EDC是由△ADB旋转180°所得,则AB边的取值范围是( )
如图所示,△ABC中,AC=5,中线AD=7,△EDC是由△ADB旋转180°所得,则AB边的取值范围是( )| A、1<AB<29 |
| B、4<AB<24 |
| C、5<AB<19 |
| D、9<AB<19 |
 如图,?ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),顶点C,D在双曲线y=
如图,?ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),顶点C,D在双曲线y=
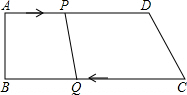 在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=25cm,BC=26cm;点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时另一个动点也停止运动,从运动开始.使PQ=CD,需经过多少时间?
在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=25cm,BC=26cm;点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时另一个动点也停止运动,从运动开始.使PQ=CD,需经过多少时间? 如图为二次函数y=ax2+bx+c的图象,有下列说法:
如图为二次函数y=ax2+bx+c的图象,有下列说法: 如图,已知点A、点B以及直线l,
如图,已知点A、点B以及直线l,