题目内容
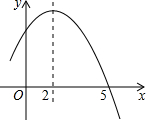如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c≥0的解集是（ ）| A、-1≤x≤5 |
| B、x≥5 |
| C、x≤-1 |
| D、x≤-1或x≥5 |
考点：二次函数与不等式（组）
专题：
分析：根据二次函数的对称性求出函数图象与x轴的另一交点的坐标，然后写出函数图象x轴上方部分的x的取值范围即可．
解答：解：由图可知，函数图象的对称轴为直线x=2，与x轴的一个交点坐标为（5，0），
所以，函数图象与x轴的另一交点的坐标是（-1，0），
所以，不等式ax2+bx+c≥0的解集是-1≤x≤5．
故选A．
所以，函数图象与x轴的另一交点的坐标是（-1，0），
所以，不等式ax2+bx+c≥0的解集是-1≤x≤5．
故选A．
点评：本题考查了二次函数与不等式，主要利用了二次函数的对称性，数形结合的思想，难点在于求出函数图象与x轴的另一交点坐标．
练习册系列答案
阅读快车系列答案
相关题目
已知一次函数y=ax+2与y=kx+b的图象如图所示，且方程组
如图，?ABCD的顶点A，B的坐标分别是A（-1，0），B（0，-2），顶点C，D在双曲线y=
如图，已知直线a，b被直线c所截，a∥b，∠2=50°，则∠1=（ ）| A、50° | B、130° |
| C、40° | D、60° |