题目内容
12.观察下列数据:-$\frac{2}{3}$,$\frac{3}{9}$,-$\frac{4}{27}$,$\frac{5}{81}$…则第n个数为(-1)n$\frac{n+1}{{3}^{n}}$.分析 根据已知发现规律,奇数项为负,偶数项为正,分母为3n,分子为n+1,由此可得结果.
解答 解:∵奇数项为负,偶数项为正,分母为3n,分子为n+1,
∴第n个数为(-1)n$\frac{n+1}{{3}^{n}}$,
故答案为:(-1)n$\frac{n+1}{{3}^{n}}$.
点评 本题主要考查了数字的变化规律,根据已知发现每项符号,分子,分母的变化规律是解答此题的关键.

练习册系列答案
相关题目
20.已知圆柱的底面半径为3cm,母线长为6cm,则圆柱的侧面积是( )
| A. | 36cm2 | B. | 36π cm2 | C. | 18cm2 | D. | 18π cm2 |
17.探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写表:
(2)写出第n个“T”字形图案中棋子的个数(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)
用棋子摆成的“T”字形图如图所示:

(1)填写表:
| 图形序号 | ① | ② | ③ | ④ | … | ⑩ |
| 每个图案中棋子个数 | 5 | 8 | … |
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)
4.下列每组数分别表示三根木棒的长度,将它们首尾连接后,不能摆成三角形的一组是( )
| A. | 2,3,5 | B. | 3,4,6 | C. | 4,5,7 | D. | 5,6,8 |
1.用科学记数法表示-37800000正确的是( )
| A. | -378×105 | B. | -3.78×107 | C. | 3.78×107 | D. | -37.8×106 |
2. 如图所示,为估计池塘两岸A,B间的距离,一位同学在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么A,B间的距离不可能是( )
如图所示,为估计池塘两岸A,B间的距离,一位同学在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么A,B间的距离不可能是( )
 如图所示,为估计池塘两岸A,B间的距离,一位同学在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么A,B间的距离不可能是( )
如图所示,为估计池塘两岸A,B间的距离,一位同学在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么A,B间的距离不可能是( )| A. | 15m | B. | 18m | C. | 26m | D. | 30m |
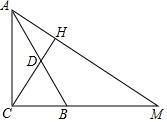 如图,在Rt△ABC中,∠ACB=90°,点D为边AB的中点,过点A作直线CD的垂线交CD的延长线于点H,交CB的延长线于点M.
如图,在Rt△ABC中,∠ACB=90°,点D为边AB的中点,过点A作直线CD的垂线交CD的延长线于点H,交CB的延长线于点M.