Question

2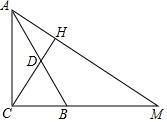．如图，在Rt△ABC中，∠ACB=90°，点D为边AB的中点，过点A作直线CD的垂线交CD的延长线于点H，交CB的延长线于点M．
（1）求证：AH•AB=AC•BC；
（2）求证：HM•AB=CH•AM．

Answer 1

分析 （1）欲证明AH•AB=AC•BC，只要证明△CAH∽△ABC即可．
（2）由S_△ACM=$\frac{1}{2}$•AM•CH=$\frac{1}{2}$•AC•CM，推出AM•CH=AC•CM，再证明△MCH∽△ABC，得到$\frac{MC}{AB}$=$\frac{MH}{AC}$，推出MC•AC=AB•MH，由此即可证明．

解答 证明：（1）∵∠ACB=90°，AD=DB，
∴CD=DA=DB，
∴∠CAD=∠ACD，
∵CH⊥AM，
∴∠AHC=∠ACB=90°，
∴△CAH∽△ABC，
∴$\frac{CA}{AB}$=$\frac{AH}{BC}$，
∴AH•AB=AC•BC．

（2）∵S_△ACM=$\frac{1}{2}$•AM•CH=$\frac{1}{2}$•AC•CM，
∴AM•CH=AC•CM，
∵CD=BD，
∴∠HCM=∠ABC，∵∠CHM=∠ACB=90°，
∴△MCH∽△ABC，
∴$\frac{MC}{AB}$=$\frac{MH}{AC}$，
∴MC•AC=AB•MH，
∴HM•AB=CH•AM．

点评 本题考查相似三角形的判定和性质、直角三角形面积的两种求法等知识，解题的关键是灵活应用所学知识解决问题，属于中考常考题型．