题目内容
3.已知y=$\sqrt{x-2}$+$\sqrt{2-x}$+1,则$\sqrt{(-2xy)^{2}}$=4.分析 根据二次根式有意义的条件可得$\left\{\begin{array}{l}{x-2≥0}\\{2-x≥0}\end{array}\right.$,解不等式组可得x=2,进而可得y的值,然后再代入$\sqrt{(-2xy)^{2}}$计算即可.
解答 解:由题意得:$\left\{\begin{array}{l}{x-2≥0}\\{2-x≥0}\end{array}\right.$,
解得:x=2,
则y=1,
$\sqrt{(-2xy)^{2}}$=$\sqrt{(-2×2×1)^{2}}$=4,
故答案为:4.
点评 此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.

练习册系列答案
相关题目
14.下列运算正确的是( )
| A. | 3a+2b=5ab | B. | 3a2b-3ba2=0 | C. | 3x2+2x3=5x5 | D. | 5y2-4y2=1 |
8.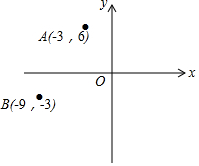 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为3:1,把△ABO放大,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为3:1,把△ABO放大,则点A的对应点A′的坐标是( )
 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为3:1,把△ABO放大,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为3:1,把△ABO放大,则点A的对应点A′的坐标是( )| A. | (-1,2) | B. | (-9,18) | C. | (-9,18)或(9,-18) | D. | (-1,2)或(1,-2) |