题目内容
2．对于任意的正整数n，能整除代数式（3n+1）（3n-1）-（3-n）（3+n）的整数是（ ）| A． | 3 | B． | 6 | C． | 10 | D． | 9 |
分析 根据平方差公式，可化简整式，根据提取公因式，可得因数．
解答 解：解：（3n+1）（3n-1）-（3-n）（3+n）=9n2-1-（9-n2）
=10n2-10
=10（n2-1），
10能整除（3n+1）（3n-1）-（3-n）（3+n），
故选C．
点评 本题考查了平方差公式，利用了平方差公式，提公因式分解因式，熟记平方差公式是解题的关键．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
12．某超市一月份的营业额为200万元，一月、二月、三月的营业额共1000万元，如果平均每月增长率为x，则根据题意列方程为（ ）
| A． | 200（1+x）2=1000 | B． | 200+200（1+x）2=1000 | ||
| C． | 200（1+x）3=1000 | D． | 200+200（1+x）+200（1+x）2=1000 |
13．
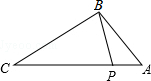如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（ ）
如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（ ）| A． | ∠ABP=∠C | B． | ∠APB=∠ABC | C． | AB2=AP•AC | D． | AB•BC=AC•BP |
如图是一正方体展开图，原正方体相对两面上的数之和是6，则a-（2b-3c）=13．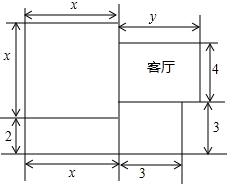
如图是一所住宅的建筑平面图（图中长度单位：m），其中客厅的面积为20m3，这所住宅的建筑面积为S．