题目内容
13.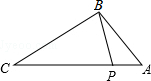 如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | AB2=AP•AC | D. | AB•BC=AC•BP |
分析 分别利用相似三角形的判定方法判断得出即可.
解答 解:A、当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
B、当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
C、当AB2=AP•AC时,则$\frac{AB}{AC}$=$\frac{AP}{AB}$,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;
D、当AB•BC=AC•BP时,则$\frac{AB}{BP}$=$\frac{AC}{BC}$,无法得到△ABP∽△ACB,故此选项正确.
故选D.
点评 本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.

练习册系列答案
相关题目
3.下列说法中正确的是( )
| A. | 单项式-$\frac{2}{3}$a2b的系数为-2 | B. | 多项式-3a2b+7a2b2+1的次数是3 | ||
| C. | a和0都是单项式 | D. | x2+$\frac{2}{y}$是整式 |
2.对于任意的正整数n,能整除代数式(3n+1)(3n-1)-(3-n)(3+n)的整数是( )
| A. | 3 | B. | 6 | C. | 10 | D. | 9 |
3.下列合并同类项中,正确的是( )
| A. | 2x+3y=5xy | B. | x2-3x2=-2x2 | C. | -2x2+2x2=x2 | D. | 3x2+2x3=5x5 |
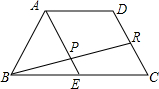 如图,AD∥BC,BC=2AD,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=$\frac{1}{3}$.
如图,AD∥BC,BC=2AD,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=$\frac{1}{3}$.