题目内容
16.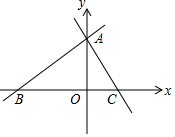 如图,在平面直角坐标系中,直线AC:y=-x+2.5与x轴交于C点,与y轴交于A点,直线AB与x轴交于C点,与y轴交于A点,已知B(-3,0).
如图,在平面直角坐标系中,直线AC:y=-x+2.5与x轴交于C点,与y轴交于A点,直线AB与x轴交于C点,与y轴交于A点,已知B(-3,0).(1)求直线AB的解析式.
(2)直线AD过点A,交线段BC于点D,把s△ABC的面积分为1:2两部分;求出此时的点D的坐标.
分析 (1)在直线AC:y=-x+2.5中,令x=0,求出A点坐标,再根据待定系数法可求直线AB的解析式.
(2)根据等高的三角形面积比等于底边的比可求点D的坐标.
解答 解:(1)在直线AC:y=-x+2.5中,令x=0,则y=2.5,
则A点坐标为(0,2.5),
设直线AB的解析式为y=kx+b,则
$\left\{\begin{array}{l}{b=2.5}\\{-3k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{5}{6}}\\{b=2.5}\end{array}\right.$.
故直线AB的解析式为y=$\frac{5}{6}$x+2.5.
(2)在直线AC:y=-x+2.5中,令y=0,则x=2.5,
则C点坐标为(2.5,0),
BC=2.5-(-3)=5.5,
5.5×$\frac{1}{1+2}$=$\frac{11}{6}$,
则点D的坐标为(-3+$\frac{11}{6}$,0)或(2.5-$\frac{11}{6}$,0),即(-$\frac{7}{6}$,0)或($\frac{2}{3}$,0).
点评 本题考查了待定系数法求一次函数解析式、一次函数图象上点的坐标特征、三角形的面积等知识,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
7.已知点C在直线AB上,点D是线段AC的中点,若AB=12,BC=5,则线段BD的长度为( )
| A. | 8.5 | B. | 3.5 | C. | 8.5或3.5 | D. | 8.3或3.7 |
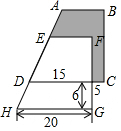 如图所示,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,平移的距离为线段AE的长,求阴影部分的面积.(单位:cm)
如图所示,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,平移的距离为线段AE的长,求阴影部分的面积.(单位:cm)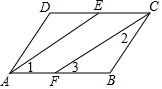 如图,已知∠DAB=∠BCD,AE平分∠DAB,CF平分∠BCD,AE∥CF,试说明∠2=∠3的理由.
如图,已知∠DAB=∠BCD,AE平分∠DAB,CF平分∠BCD,AE∥CF,试说明∠2=∠3的理由.