题目内容
 如图,在等边△ABC中,O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中除△ABC外等腰三角形的个数是( )
如图,在等边△ABC中,O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中除△ABC外等腰三角形的个数是( )| A、7 | B、6 | C、5 | D、4 |
考点:等腰三角形的判定,等边三角形的性质
专题:
分析:证明OA=OB=OC;证明DB=DO,OE=CE;证明OD=OE;即可解决问题.
解答: 解:∵点O是等边△ABC的内心,
解:∵点O是等边△ABC的内心,
∴OA=OB=OC;∠OBA=∠OBD=30°;
∵OD∥AB,OE∥AC,
∴∠DOB=∠OBA=30°,
∴∠OBD=∠BOD,DB=DO;
同理可证:OE=CE;
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC,∠OED=∠ACB=60°,
∴∠ODE=∠OED,OD=OE;
∴△AOB、△AOC、△BOC,
△BOD、△COE、△ODE均为等腰三角形.
故选B.
 解:∵点O是等边△ABC的内心,
解:∵点O是等边△ABC的内心,∴OA=OB=OC;∠OBA=∠OBD=30°;
∵OD∥AB,OE∥AC,
∴∠DOB=∠OBA=30°,
∴∠OBD=∠BOD,DB=DO;
同理可证:OE=CE;
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC,∠OED=∠ACB=60°,
∴∠ODE=∠OED,OD=OE;
∴△AOB、△AOC、△BOC,
△BOD、△COE、△ODE均为等腰三角形.
故选B.
点评:该题主要考查了等边三角形的性质、等腰三角形的判定、平行线的性质及其应用问题;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
相关题目
下列关于x的函数中,一定是二次函数的是( )
| A、y=ax2+bx+c | ||
B、y=x2+
| ||
| C、y=2x+c2 | ||
| D、y=(x-k)2+h |
 如图,把长方形ABCD沿EF按图那样折叠后,A、B分别落在G、H点处,若∠1=50°,则∠AEF=( )
如图,把长方形ABCD沿EF按图那样折叠后,A、B分别落在G、H点处,若∠1=50°,则∠AEF=( )| A、110° | B、115° |
| C、120° | D、125° |
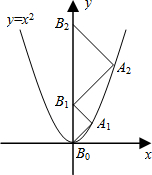 如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )
如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )| A、2013 | ||
| B、2014 | ||
C、2013
| ||
D、2014
|
若分式
中的x、y同时扩大3倍,则分式的值( )
| x+2y |
| x |
| A、扩大3倍 | ||
| B、扩大9倍 | ||
| C、不变 | ||
D、缩小为原来的
|
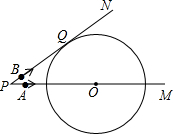 如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为t s.当t=
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为t s.当t= 如图,AB是⊙O的直径,AD、BC和CD分别与⊙O相切于点A、B和E,DA=3.6,CB=6.4,
如图,AB是⊙O的直径,AD、BC和CD分别与⊙O相切于点A、B和E,DA=3.6,CB=6.4,