题目内容
如图，把长方形ABCD沿EF按图那样折叠后，A、B分别落在G、H点处，若∠1=50°，则∠AEF=（ ）| A、110° | B、115° |
| C、120° | D、125° |
考点：平行线的性质,翻折变换（折叠问题）
专题：
分析：如图，证明∠AEF+∠BFE=180°；借助翻折变换的性质求出∠BFE，即可解决问题．
解答：解：如图，
∵四边形ABCD为长方形，
∴AE∥BF，∠AEF+∠BFE=180°；
由折叠变换的性质得：
∠BFE=∠HFE，而∠1=50°，
∴∠BFE=（180°-50°）÷2=65°，
∴∠AEF=180°-65°=115°．
故选B．
解：如图，∵四边形ABCD为长方形，
∴AE∥BF，∠AEF+∠BFE=180°；
由折叠变换的性质得：
∠BFE=∠HFE，而∠1=50°，
∴∠BFE=（180°-50°）÷2=65°，
∴∠AEF=180°-65°=115°．
故选B．
点评：该题主要考查了翻折变换的性质、矩形的性质、平行线的性质及其应用问题；应牢固掌握、矩形的性质、平行线的性质等几何知识点．
练习册系列答案
相关题目
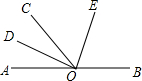如图，O为直线AB上一点，OD平分∠AOC，∠DOE=90°．
如图，?ABCD中，AE⊥BC于E，AF⊥CD于F，若AE=4，AF=6，sin∠BAE=若
=
，则
=（ ）
| m+n |
| m-n |
| 7 |
| 3 |
| m |
| m-n |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在等边△ABC中，O是三个内角平分线的交点，OD∥AB，OE∥AC，则图中除△ABC外等腰三角形的个数是（ ）
如图，在图1中，各行，各列及对角线上三个数之和都相等．