题目内容
2.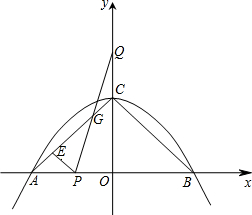 如图,二次函数y=-$\frac{1}{2}{x^2}$+2与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动.设PQ交直线AC于点G.
如图,二次函数y=-$\frac{1}{2}{x^2}$+2与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动.设PQ交直线AC于点G.(1)求直线AC的解析式;
(2)设△PQC的面积为S,求S关于t的函数解析式;
(3)在y轴上找一点M,使△MAC和△MBC都是等腰三角形.直接
写出所有满足条件的M点的坐标;
(4)过点P作PE⊥AC,垂足为E,当P点运动时,线段EG的长度
是否发生改变,请说明理由.
分析 (1)直线AC经过点A,C,根据抛物线的解析式面积可求得两点坐标,利用待定系数法就可求得AC的解析式;
(2)根据三角形面积公式即可写出解析式;
(3)可以分腰和底边进行讨论,即可确定点的坐标;
(4)过G作GH⊥y轴,根据三角形相似,相似三角形的对应边的比相等即可求解.
解答  解:(1)∵二次函数y=-$\frac{1}{2}{x^2}$+2,
解:(1)∵二次函数y=-$\frac{1}{2}{x^2}$+2,
∴A点的坐标为(-2,0),与y轴交于点C(0,2),
∴c=2,
设直线AC的解析式是y=kx+b,由题意可知
$\left\{\begin{array}{l}{-2k+b=0}\\{b=2}\end{array}\right.$,
解得:k=1,b=2,
即直线AC的解析式是y=x+2;
(2)当0<t<2时,
OP=(2-t),QC=t,
∴△PQC的面积为:S=$\frac{1}{2}$(2-t)t=-$\frac{1}{2}$t2+t,
当2<t≤4时,
OP=(t-2),QC=t,
∴△PQC的面积为:S=$\frac{1}{2}$(t-2)t=$\frac{1}{2}$t2-t,
(3))∵A(-2,0),B(2,0),C(0,2),
∴OA=OB=OC=2,
根据勾股定理,AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
如图,①点M为坐标原点(0,0)时,AC、BC为底边,
②AC、BC为底边时,若OM=OC=2,则点M(0,-2),
若CM=AC=2$\sqrt{2}$,则OM=CM-OC=2$\sqrt{2}$-2,
此时点M(0,2-2$\sqrt{2}$),
或OM=CM+OC=2$\sqrt{2}$+2,
此时点M(0,2+2$\sqrt{2}$),
所以,点M的坐标为(0,0)或(0,-2)或(0,2-2$\sqrt{2}$)或(0,2+2$\sqrt{2}$).
(4)当P点运动时,线段EG的长度不变EG=$\sqrt{2}$,
理由如下:当0<t<2时,过G作GH⊥y轴,垂足为H.
由AP=t,可得AE=$\frac{\sqrt{2}}{2}$t,
由$\frac{GH}{PO}=\frac{QH}{QO}$即$\frac{GH}{2-t}=\frac{GH+t}{2+t}$,
解得:GH=1-$\frac{1}{2}$t,
∴CG=$\sqrt{2}$GH=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$t,
∴GE=AC-AE-GC=2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$t-($\sqrt{2}$-$\frac{\sqrt{2}}{2}$t)=$\sqrt{2}$,
即GE的长度不变.
当2<t≤4时,过G作GH⊥y轴,垂足为H.
由AP=t,可得AE=$\frac{\sqrt{2}}{2}$t,
由$\frac{GH}{PO}=\frac{QH}{QO}$即$\frac{GH}{t-2}=\frac{t-GH}{2+t}$,
∴GH(2+t)=t(t-2)-(t-2)GH,
∴GH(2+t)+(t-2)GH=t(t-2),
∴2tGH=t(t-2),
解得GH=$\frac{t-2}{2}$,
∴CG=$\sqrt{2}$GH=$\frac{\sqrt{2}(t-2)}{2}$,
于是,GE=AC-AE+GC=2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$t+$\frac{\sqrt{2}(t-2)}{2}$=$\sqrt{2}$,
即GE的长度不变.
综合得:当P点运动时,线段EG的长度不发生改变,为定值$\sqrt{2}$.
点评 本题考查用待定系数法求二次函数和一次函数的解析式以及三角形的面积公式和相似三角形的性质,解题的难点在于分类讨论的数学思想的运用,要做到不重不漏的分析问题的存在性.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 收益变化/元 | +0.01 | +0.01 | -0.02 | -0.04 | -0.01 | +0.01 | +0.03 |
②上星期日的收益为1.5元.
(1)请你通过计算说明该星期日与上星期日相比,收益增加了还是减少了?如果增加了,求出增加的钱数,如果减少了,求出减少的钱数.
(2)求这一周玲玲总共收益的钱数.
| A. | 3x2-5=1 | B. | 2x2+x+1 | C. | 4x-9y=0 | D. | x+y=0 |
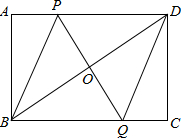 如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.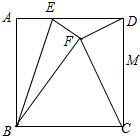 E是正方形ABCD的边AD上一点,将△ABE沿直线BE对折,使点A落在点F处,连接CF,DF.若∠DFC=90°,求$\frac{AE}{ED}$的值.
E是正方形ABCD的边AD上一点,将△ABE沿直线BE对折,使点A落在点F处,连接CF,DF.若∠DFC=90°,求$\frac{AE}{ED}$的值.