题目内容
7.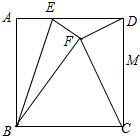 E是正方形ABCD的边AD上一点,将△ABE沿直线BE对折,使点A落在点F处,连接CF,DF.若∠DFC=90°,求$\frac{AE}{ED}$的值.
E是正方形ABCD的边AD上一点,将△ABE沿直线BE对折,使点A落在点F处,连接CF,DF.若∠DFC=90°,求$\frac{AE}{ED}$的值.
分析 延长EF交CD于M,连接BM,根据正方形的性质得到AB=BC,∠A=∠BCD=90°由折叠的性质得到∠BFE=∠BFM=90°,通过Rt△BFM≌Rt△BCM,于是得到MF=MC.由等腰三角形的性质得到∠MFC=∠MCF由余角的性质得到∠MFC=∠MDF,于是求得MF=MD,设MF=MD=MC=a,AE=EF=x根据勾股定理即可得到结论.
解答  解:延长EF交CD于M,连接BM,
解:延长EF交CD于M,连接BM,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠BCD=90°,
∵将△ABE沿直线BE对折得到△BEF,
∴∠BFE=∠BFM=90°,
在Rt△BFM与Rt△BCM中,$\left\{\begin{array}{l}{BF=BC}\\{BM=BM}\end{array}\right.$,
∴Rt△BFM≌Rt△BCM,
∴MF=MC,
∴∠MFC=∠MCF,
∵∠MFC+∠DFM=90°,∠MCF+∠FDM=90°,
∴∠MFC=∠MDF,
∴MF=MD,
设MF=MD=MC=a,AE=EF=x,
∵DE2+DM2=EM2,
即(2a-x)2+a2=(x+a)2,
解得:x=$\frac{2}{3}$a,
∴AE=$\frac{2}{3}$a,DE=$\frac{4}{3}$a,
∴$\frac{AE}{ED}$=$\frac{1}{2}$.
点评 本题考查了翻折变换-折叠问题,正方形的性质,全等三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
18.若关于x的分式方程$\frac{m}{x-5}$=$\frac{x-1}{x-5}$无解,则m的值为( )
| A. | -4 | B. | 4 | C. | -6 | D. | 6 |
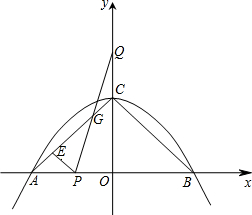 如图,二次函数y=-$\frac{1}{2}{x^2}$+2与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动.设PQ交直线AC于点G.
如图,二次函数y=-$\frac{1}{2}{x^2}$+2与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动.设PQ交直线AC于点G.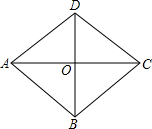 如图,菱形ABCD中,AC、BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线动动到C,动点N从B出发沿BD方向以1m/s匀速直线动动到D,若M、N同进出发,则出发后$\frac{5-\sqrt{2}}{2}$s或$\frac{5}{2}$s或$\frac{5+\sqrt{2}}{2}$s时,△MON的面积为$\frac{1}{4}$m2.
如图,菱形ABCD中,AC、BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线动动到C,动点N从B出发沿BD方向以1m/s匀速直线动动到D,若M、N同进出发,则出发后$\frac{5-\sqrt{2}}{2}$s或$\frac{5}{2}$s或$\frac{5+\sqrt{2}}{2}$s时,△MON的面积为$\frac{1}{4}$m2.