题目内容
11.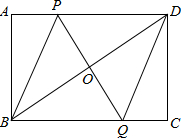 如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.(1)求证:△POD≌△QOB;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/s的速度向D运动(不与D重合).设点P运动时间为t秒,请用t表示PD的长;并求出t为何值时,四边形PBQD是菱形.
分析 (1)先根据矩形性质得AD∥BC,则∠PDB=∠QBD,于是可根据“ASA”证明△POD≌△QOB;
(2)AP=t,PD=AD-AP=8-t,由△POD≌△QOB得到OP=OQ,于是可判断四边形PBQD为平行四边形,根据菱形的判定方法,当PB=PD时,四边形PBQD是菱形,则PB=8-t,然后在Rt△ABP中利用勾股定理得到62+t2=(8-t)2,然后解方程求出t即可.
解答 (1)证明:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠PDB=∠QBD,
在△POD和△QOB中,
$\left\{\begin{array}{l}{∠PDO=∠QBO}\\{OD=OB}\\{∠POD=∠QOB}\end{array}\right.$,
∴△POD≌△QOB;
(2)解:AP=t,PD=AD-AP=8-t,
∵△POD≌△QOB,
∴OP=OQ,
而OD=OB,
∴四边形PBQD为平行四边形,
∴当PB=PD时,四边形PBQD是菱形,
则PB=8-t,
在Rt△ABP中,∵AB2+AP2=PB2,
∴62+t2=(8-t)2,解得t=$\frac{7}{4}$,
即当t为$\frac{7}{4}$s时,四边形PBQD是菱形.
点评 本题考查了菱形的判定:一组邻边相等的平行四边形是菱形;四条边都相等的四边形是菱形;对角线互相垂直的平行四边形是菱形.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
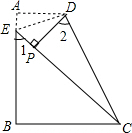 下图是一张四边形ABCD纸片,∠A=90°,AD∥BC,沿虚线DE折叠,使点A落在四边形DEBC的内部点P处.
下图是一张四边形ABCD纸片,∠A=90°,AD∥BC,沿虚线DE折叠,使点A落在四边形DEBC的内部点P处. 如图,△ABC中,CA=CB,D为△ABC内一点,∠1=∠2,若∠C=40°,求∠ADB的度数.
如图,△ABC中,CA=CB,D为△ABC内一点,∠1=∠2,若∠C=40°,求∠ADB的度数.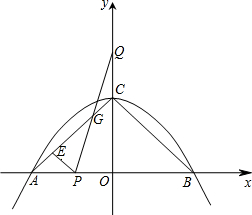 如图,二次函数y=-$\frac{1}{2}{x^2}$+2与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动.设PQ交直线AC于点G.
如图,二次函数y=-$\frac{1}{2}{x^2}$+2与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动.设PQ交直线AC于点G.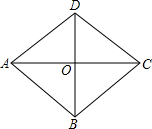 如图,菱形ABCD中,AC、BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线动动到C,动点N从B出发沿BD方向以1m/s匀速直线动动到D,若M、N同进出发,则出发后$\frac{5-\sqrt{2}}{2}$s或$\frac{5}{2}$s或$\frac{5+\sqrt{2}}{2}$s时,△MON的面积为$\frac{1}{4}$m2.
如图,菱形ABCD中,AC、BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线动动到C,动点N从B出发沿BD方向以1m/s匀速直线动动到D,若M、N同进出发,则出发后$\frac{5-\sqrt{2}}{2}$s或$\frac{5}{2}$s或$\frac{5+\sqrt{2}}{2}$s时,△MON的面积为$\frac{1}{4}$m2.