题目内容
已知等腰△ABC的周长为8,腰长为x,底边长为y.
(1)写出y关于x的函数关系式,并求自变量x的取值范围;
(2)在平面直角坐标系中,画出y与x之间的函数图像;
(3)若△ABC的三边长均为整数,求三边的长.
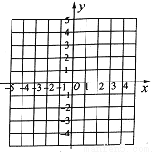
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
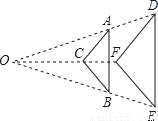
如图,△ABC与△DEF是位似图形,位似比为2:3,已知AB=4,则DE的长为_____.
下表是围外城市与北京的时差(带正号的数表示同一时刻比北京时涧早的时数)如果现在是北京时间10:00,那么巴黎时间是____________.
城市 | 纽约 | 巴黎 | 东京 | 多伦多 |
时差(时) | -13 | -7 | +1 | -12 |


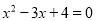 的根的情况是( )
的根的情况是( )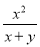 中的x、y的值同时扩大3倍,则分式的值( )
中的x、y的值同时扩大3倍,则分式的值( )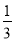
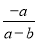 可变形为( )
可变形为( )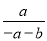 B.
B. 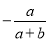 C.
C. 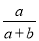 D.
D. 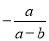
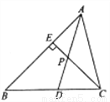
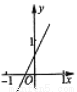 B.
B. 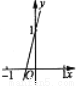 C.
C. 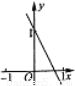 D.
D. 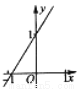
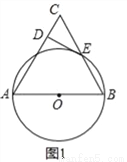
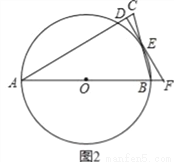
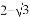 ,求⊙O的半径和BF的长
,求⊙O的半径和BF的长